You are given a tree rooted at node 0, consisting of n nodes numbered from 0 to n - 1. The tree is represented by an array parent of size n, where parent[i] is the parent of node i. Since node 0 is the root, parent[0] == -1.
You are also given a string s of length n, where s[i] is the character assigned to node i.
Consider an empty string dfsStr, and define a recursive function dfs(int x) that takes a node x as a parameter and performs the following steps in order:
y of x in increasing order of their numbers, and call dfs(y).s[x] to the end of the string dfsStr.Note that dfsStr is shared across all recursive calls of dfs.
You need to find a boolean array answer of size n, where for each index i from 0 to n - 1, you do the following:
dfsStr and call dfs(i).dfsStr is a palindrome, then set answer[i] to true. Otherwise, set answer[i] to false.Return the array answer.
Example 1:
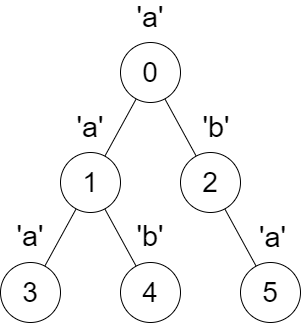
Input: parent = [-1,0,0,1,1,2], s = "aababa"
Output: [true,true,false,true,true,true]
Explanation:
dfs(0) results in the string dfsStr = "abaaba", which is a palindrome.dfs(1) results in the string dfsStr = "aba", which is a palindrome.dfs(2) results in the string dfsStr = "ab", which is not a palindrome.dfs(3) results in the string dfsStr = "a", which is a palindrome.dfs(4) results in the string dfsStr = "b", which is a palindrome.dfs(5) results in the string dfsStr = "a", which is a palindrome.Example 2:
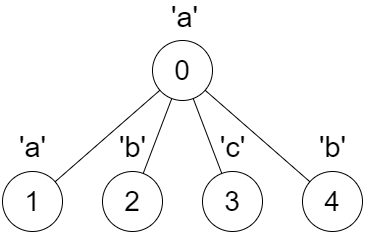
Input: parent = [-1,0,0,0,0], s = "aabcb"
Output: [true,true,true,true,true]
Explanation:
Every call on dfs(x) results in a palindrome string.
Constraints:
n == parent.length == s.length1 <= n <= 1050 <= parent[i] <= n - 1 for all i >= 1.parent[0] == -1parent represents a valid tree.s consists only of lowercase English letters.