Input: grid = [[1,4],[2,3]]
Output: true
Explanation:
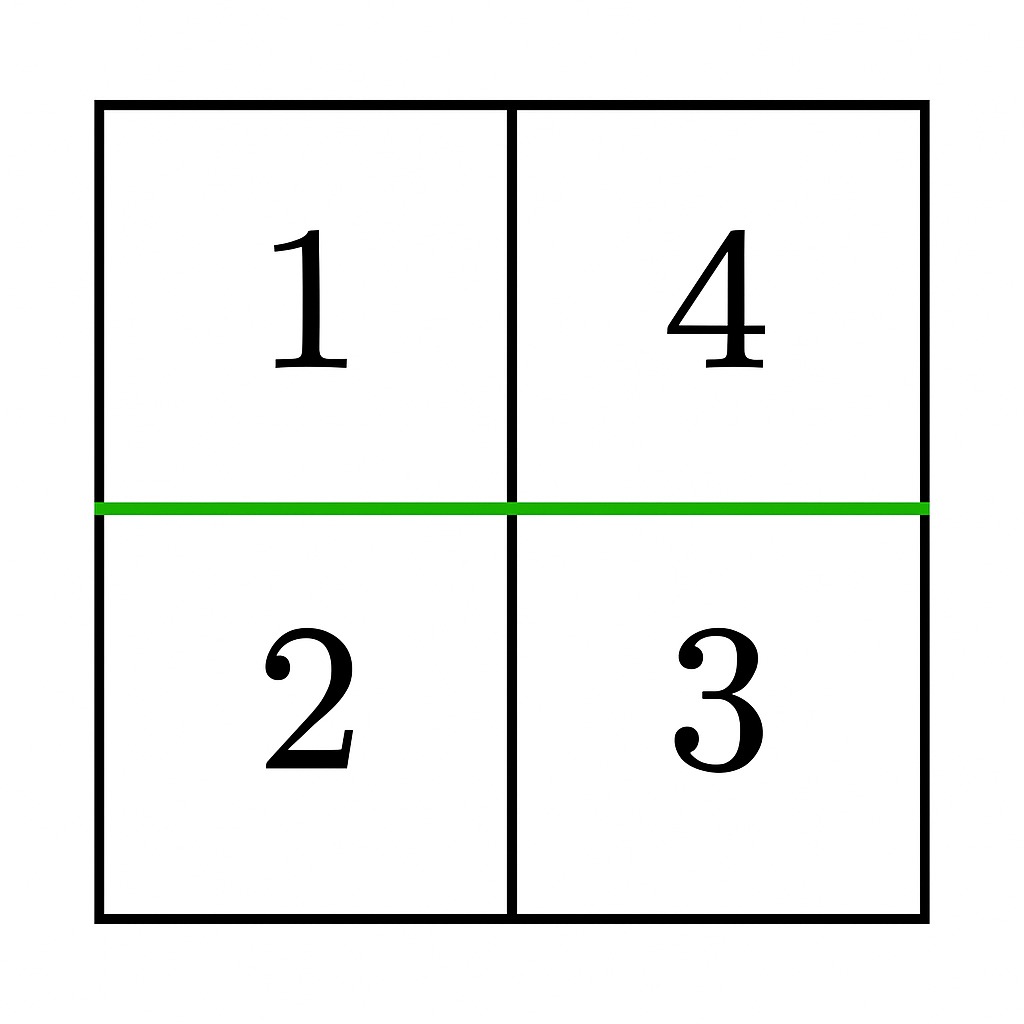
- A horizontal cut after the first row gives sums
1 + 4 = 5and2 + 3 = 5, which are equal. Thus, the answer istrue.
You are given an m x n matrix grid of positive integers. Your task is to determine if it is possible to make either one horizontal or one vertical cut on the grid such that:
Return true if such a partition exists; otherwise, return false.
Note: A section is connected if every cell in it can be reached from any other cell by moving up, down, left, or right through other cells in the section.
Example 1:
Input: grid = [[1,4],[2,3]]
Output: true
Explanation:

1 + 4 = 5 and 2 + 3 = 5, which are equal. Thus, the answer is true.Example 2:
Input: grid = [[1,2],[3,4]]
Output: true
Explanation:
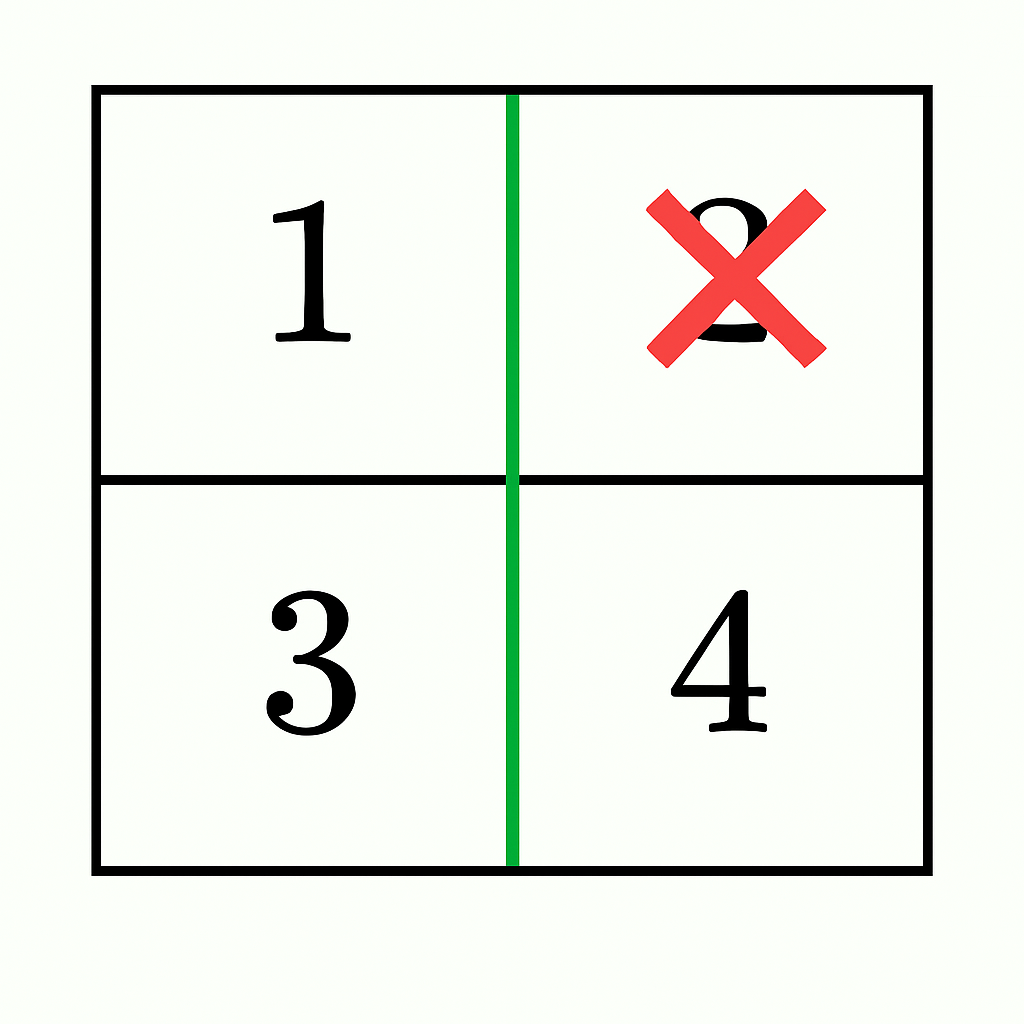
1 + 3 = 4 and 2 + 4 = 6.6 - 2 = 4), both sections have equal sums and remain connected. Thus, the answer is true.Example 3:
Input: grid = [[1,2,4],[2,3,5]]
Output: false
Explanation:
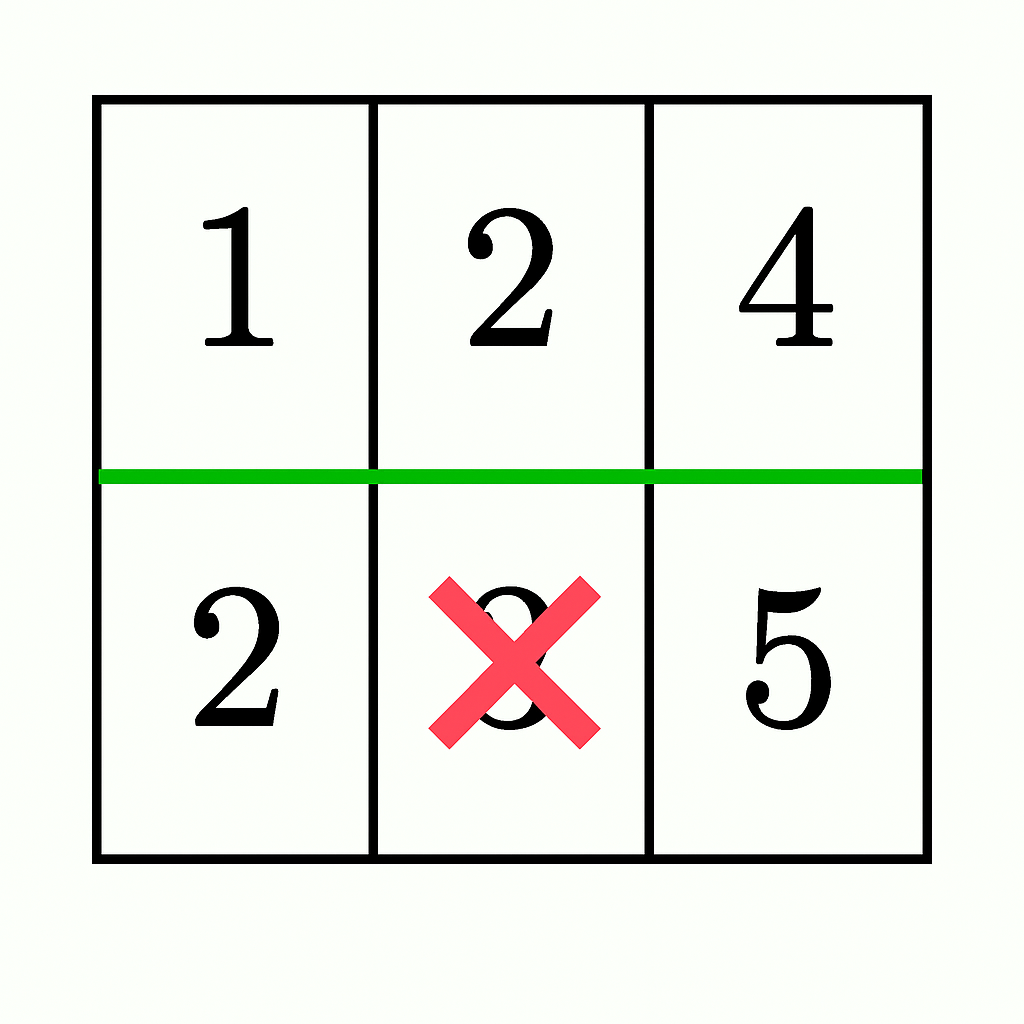
1 + 2 + 4 = 7 and 2 + 3 + 5 = 10.10 - 3 = 7), both sections have equal sums, but they do not remain connected as it splits the bottom section into two parts ([2] and [5]). Thus, the answer is false.Example 4:
Input: grid = [[4,1,8],[3,2,6]]
Output: false
Explanation:
No valid cut exists, so the answer is false.
Constraints:
1 <= m == grid.length <= 1051 <= n == grid[i].length <= 1052 <= m * n <= 1051 <= grid[i][j] <= 105