输入: n = 4, edges = [[0,1,3],[3,1,1],[2,3,4],[0,2,2]]
输出: 5
解释:
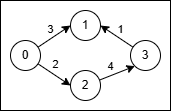
- 使用路径
0 → 1(成本 3)。 - 在节点 1,将原始边
3 → 1反转为1 → 3并穿过它,成本为2 * 1 = 2。 - 总成本为
3 + 2 = 5。
给你一个包含 n 个节点的有向带权图,节点编号从 0 到 n - 1。同时给你一个数组 edges,其中 edges[i] = [ui, vi, wi] 表示一条从节点 ui 到节点 vi 的有向边,其成本为 wi。
每个节点 ui 都有一个 最多可使用一次 的开关:当你到达 ui 且尚未使用其开关时,你可以对其一条入边 vi → ui 激活开关,将该边反转为 ui → vi 并 立即 穿过它。
反转仅对那一次移动有效,使用反转边的成本为 2 * wi。
返回从节点 0 到达节点 n - 1 的 最小 总成本。如果无法到达,则返回 -1。
示例 1:
输入: n = 4, edges = [[0,1,3],[3,1,1],[2,3,4],[0,2,2]]
输出: 5
解释:

0 → 1 (成本 3)。3 → 1 反转为 1 → 3 并穿过它,成本为 2 * 1 = 2。3 + 2 = 5。示例 2:
输入: n = 4, edges = [[0,2,1],[2,1,1],[1,3,1],[2,3,3]]
输出: 3
解释:
0 → 2 (成本 1),然后 2 → 1 (成本 1),再然后 1 → 3 (成本 1)。1 + 1 + 1 = 3。
提示:
2 <= n <= 5 * 1041 <= edges.length <= 105edges[i] = [ui, vi, wi]0 <= ui, vi <= n - 11 <= wi <= 1000