mirror of
https://gitee.com/coder-xiaomo/leetcode-problemset
synced 2025-12-11 21:30:58 +08:00
update
This commit is contained in:
@@ -0,0 +1,73 @@
|
||||
<p>请你编写一个异步函数 <code>promisePool</code> ,它接收一个异步函数数组 <code>functions</code> 和 <strong>池限制</strong> <code>n</code>。它应该返回一个 promise 对象,当所有输入函数都执行完毕后,promise 对象就执行完毕。</p>
|
||||
|
||||
<p><strong>池限制</strong> 定义是一次可以挂起的最多 promise 对象的数量。<code>promisePool</code> 应该开始执行尽可能多的函数,并在旧的 promise 执行完毕后继续执行新函数。<code>promisePool</code> 应该先执行 <code>functions[i]</code>,再执行 <code>functions[i + 1]</code>,然后执行 <code>functions[i + 2]</code>,等等。当最后一个 promise 执行完毕时,<code>promisePool</code> 也应该执行完毕。</p>
|
||||
|
||||
<p>例如,如果 <code>n = 1</code> , <code>promisePool</code> 在序列中每次执行一个函数。然而,如果 <code>n = 2</code> ,它首先执行两个函数。当两个函数中的任何一个执行完毕后,再执行第三个函数(如果它是可用的),依此类推,直到没有函数要执行为止。</p>
|
||||
|
||||
<p>你可以假设所有的 <code>functions</code> 都不会被拒绝。对于 <code>promisePool</code> 来说,返回一个可以解析任何值的 promise 都是可以接受的。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong class="example">示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
functions = [
|
||||
() => new Promise(res => setTimeout(res, 300)),
|
||||
() => new Promise(res => setTimeout(res, 400)),
|
||||
() => new Promise(res => setTimeout(res, 200))
|
||||
]
|
||||
n = 2
|
||||
<b>输出:</b>[[300,400,500],500]
|
||||
<strong>解释</strong>
|
||||
传递了三个函数。它们的睡眠时间分别为 300ms、 400ms 和 200ms。
|
||||
在 t=0 时,执行前两个函数。池大小限制达到 2。
|
||||
当 t=300 时,第一个函数执行完毕后,执行第3个函数。池大小为 2。
|
||||
在 t=400 时,第二个函数执行完毕后。没有什么可执行的了。池大小为 1。
|
||||
在 t=500 时,第三个函数执行完毕后。池大小为 0,因此返回的 promise 也执行完成。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:
|
||||
</strong>functions = [
|
||||
() => new Promise(res => setTimeout(res, 300)),
|
||||
() => new Promise(res => setTimeout(res, 400)),
|
||||
() => new Promise(res => setTimeout(res, 200))
|
||||
]
|
||||
n = 5
|
||||
<b>输出:</b>[[300,400,200],400]
|
||||
<strong>解释:</strong>
|
||||
在 t=0 时,所有3个函数都被执行。池的限制大小 5 永远不会满足。
|
||||
在 t=200 时,第三个函数执行完毕后。池大小为 2。
|
||||
在 t=300 时,第一个函数执行完毕后。池大小为 1。
|
||||
在 t=400 时,第二个函数执行完毕后。池大小为 0,因此返回的 promise 也执行完成。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>
|
||||
functions = [
|
||||
() => new Promise(res => setTimeout(res, 300)),
|
||||
() => new Promise(res => setTimeout(res, 400)),
|
||||
() => new Promise(res => setTimeout(res, 200))
|
||||
]
|
||||
n = 1
|
||||
<b>输出:</b>[[300,700,900],900]
|
||||
<strong>解释:</strong>
|
||||
在 t=0 时,执行第一个函数。池大小为1。
|
||||
当 t=300 时,第一个函数执行完毕后,执行第二个函数。池大小为 1。
|
||||
当 t=700 时,第二个函数执行完毕后,执行第三个函数。池大小为 1。
|
||||
在 t=900 时,第三个函数执行完毕后。池大小为 0,因此返回的 Promise 也执行完成。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>0 <= functions.length <= 10</code></li>
|
||||
<li><code><font face="monospace">1 <= n <= 10</font></code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,45 @@
|
||||
<p>定义一个数组 <code>arr</code> 的 <strong>转换数组</strong> <code>conver</code> 为:</p>
|
||||
|
||||
<ul>
|
||||
<li><code>conver[i] = arr[i] + max(arr[0..i])</code>,其中 <code>max(arr[0..i])</code> 是满足 <code>0 <= j <= i</code> 的所有 <code>arr[j]</code> 中的最大值。</li>
|
||||
</ul>
|
||||
|
||||
<p>定义一个数组 <code>arr</code> 的 <strong>分数</strong> 为 <code>arr</code> 转换数组中所有元素的和。</p>
|
||||
|
||||
<p>给你一个下标从 <strong>0</strong> 开始长度为 <code>n</code> 的整数数组 <code>nums</code> ,请你返回一个长度为 <code>n</code> 的数组<em> </em><code>ans</code> ,其中 <code>ans[i]</code>是前缀 <code>nums[0..i]</code> 的分数。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre><b>输入:</b>nums = [2,3,7,5,10]
|
||||
<b>输出:</b>[4,10,24,36,56]
|
||||
<b>解释:</b>
|
||||
对于前缀 [2] ,转换数组为 [4] ,所以分数为 4 。
|
||||
对于前缀 [2, 3] ,转换数组为 [4, 6] ,所以分数为 10 。
|
||||
对于前缀 [2, 3, 7] ,转换数组为 [4, 6, 14] ,所以分数为 24 。
|
||||
对于前缀 [2, 3, 7, 5] ,转换数组为 [4, 6, 14, 12] ,所以分数为 36 。
|
||||
对于前缀 [2, 3, 7, 5, 10] ,转换数组为 [4, 6, 14, 12, 20] ,所以分数为 56 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre><b>输入:</b>nums = [1,1,2,4,8,16]
|
||||
<b>输出:</b>[2,4,8,16,32,64]
|
||||
<b>解释:</b>
|
||||
对于前缀 [1] ,转换数组为 [2] ,所以分数为 2 。
|
||||
对于前缀 [1, 1],转换数组为 [2, 2] ,所以分数为 4 。
|
||||
对于前缀 [1, 1, 2],转换数组为 [2, 2, 4] ,所以分数为 8 。
|
||||
对于前缀 [1, 1, 2, 4],转换数组为 [2, 2, 4, 8] ,所以分数为 16 。
|
||||
对于前缀 [1, 1, 2, 4, 8],转换数组为 [2, 2, 4, 8, 16] ,所以分数为 32 。
|
||||
对于前缀 [1, 1, 2, 4, 8, 16],转换数组为 [2, 2, 4, 8, 16, 32] ,所以分数为 64 。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= nums.length <= 10<sup>5</sup></code></li>
|
||||
<li><code>1 <= nums[i] <= 10<sup>9</sup></code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,41 @@
|
||||
<p>给你一个大小为 <code>m x n</code> 的二进制矩阵 <code>mat</code> ,请你找出包含最多 <strong>1</strong> 的行的下标(从 <strong>0</strong> 开始)以及这一行中 <strong>1</strong> 的数目。</p>
|
||||
|
||||
<p>如果有多行包含最多的 1 ,只需要选择 <strong>行下标最小</strong> 的那一行。</p>
|
||||
|
||||
<p>返回一个由行下标和该行中 1 的数量组成的数组。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>mat = [[0,1],[1,0]]
|
||||
<strong>输出:</strong>[0,1]
|
||||
<strong>解释:</strong>两行中 1 的数量相同。所以返回下标最小的行,下标为 0 。该行 1 的数量为 1 。所以,答案为 [0,1] 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>mat = [[0,0,0],[0,1,1]]
|
||||
<strong>输出:</strong>[1,2]
|
||||
<strong>解释:</strong>下标为 1 的行中 1 的数量最多<code>。</code>该行 1 的数量<code>为 2 。所以,答案为</code> [1,2] 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>mat = [[0,0],[1,1],[0,0]]
|
||||
<strong>输出:</strong>[1,2]
|
||||
<strong>解释:</strong>下标为 1 的行中 1 的数量最多。该行 1 的数量<code>为 2 。所以,答案为</code> [1,2] 。</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>m == mat.length</code> </li>
|
||||
<li><code>n == mat[i].length</code> </li>
|
||||
<li><code>1 <= m, n <= 100</code> </li>
|
||||
<li><code>mat[i][j]</code> 为 <code>0</code> 或 <code>1</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,47 @@
|
||||
<p>给你一棵二叉树的根 <code>root</code> ,请你将每个节点的值替换成该节点的所有 <strong>堂兄弟节点值的和 </strong>。</p>
|
||||
|
||||
<p>如果两个节点在树中有相同的深度且它们的父节点不同,那么它们互为 <strong>堂兄弟</strong> 。</p>
|
||||
|
||||
<p>请你返回修改值之后,树的根<em> </em><code>root</code><em> </em>。</p>
|
||||
|
||||
<p><strong>注意</strong>,一个节点的深度指的是从树根节点到这个节点经过的边数。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<p><img alt="" src="https://assets.leetcode.com/uploads/2023/01/11/example11.png" style="width: 571px; height: 151px;" /></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>root = [5,4,9,1,10,null,7]
|
||||
<b>输出:</b>[0,0,0,7,7,null,11]
|
||||
<b>解释:</b>上图展示了初始的二叉树和修改每个节点的值之后的二叉树。
|
||||
- 值为 5 的节点没有堂兄弟,所以值修改为 0 。
|
||||
- 值为 4 的节点没有堂兄弟,所以值修改为 0 。
|
||||
- 值为 9 的节点没有堂兄弟,所以值修改为 0 。
|
||||
- 值为 1 的节点有一个堂兄弟,值为 7 ,所以值修改为 7 。
|
||||
- 值为 10 的节点有一个堂兄弟,值为 7 ,所以值修改为 7 。
|
||||
- 值为 7 的节点有两个堂兄弟,值分别为 1 和 10 ,所以值修改为 11 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<p><img alt="" src="https://assets.leetcode.com/uploads/2023/01/11/diagram33.png" style="width: 481px; height: 91px;" /></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>root = [3,1,2]
|
||||
<b>输出:</b>[0,0,0]
|
||||
<b>解释:</b>上图展示了初始的二叉树和修改每个节点的值之后的二叉树。
|
||||
- 值为 3 的节点没有堂兄弟,所以值修改为 0 。
|
||||
- 值为 1 的节点没有堂兄弟,所以值修改为 0 。
|
||||
- 值为 2 的节点没有堂兄弟,所以值修改为 0 。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li>树中节点数目的范围是 <code>[1, 10<sup>5</sup>]</code> 。</li>
|
||||
<li><code>1 <= Node.val <= 10<sup>4</sup></code></li>
|
||||
</ul>
|
||||
60
leetcode-cn/problem (Chinese)/传送卷轴 [rdmXM7].md
Normal file
60
leetcode-cn/problem (Chinese)/传送卷轴 [rdmXM7].md
Normal file
@@ -0,0 +1,60 @@
|
||||
随着不断的深入,小扣来到了守护者之森寻找的魔法水晶。首先,他必须先通过守护者的考验。
|
||||
|
||||
考验的区域是一个正方形的迷宫,`maze[i][j]` 表示在迷宫 `i` 行 `j` 列的地形:
|
||||
- 若为 `.` ,表示可以到达的空地;
|
||||
- 若为 `#` ,表示不可到达的墙壁;
|
||||
- 若为 `S` ,表示小扣的初始位置;
|
||||
- 若为 `T` ,表示魔法水晶的位置。
|
||||
|
||||
小扣每次可以向 上、下、左、右 相邻的位置移动一格。而守护者拥有一份「传送魔法卷轴」,使用规则如下:
|
||||
- 魔法需要在小扣位于 **空地** 时才能释放,发动后卷轴消失;;
|
||||
- 发动后,小扣会被传送到水平或者竖直的镜像位置,且目标位置不得为墙壁(如下图所示);
|
||||
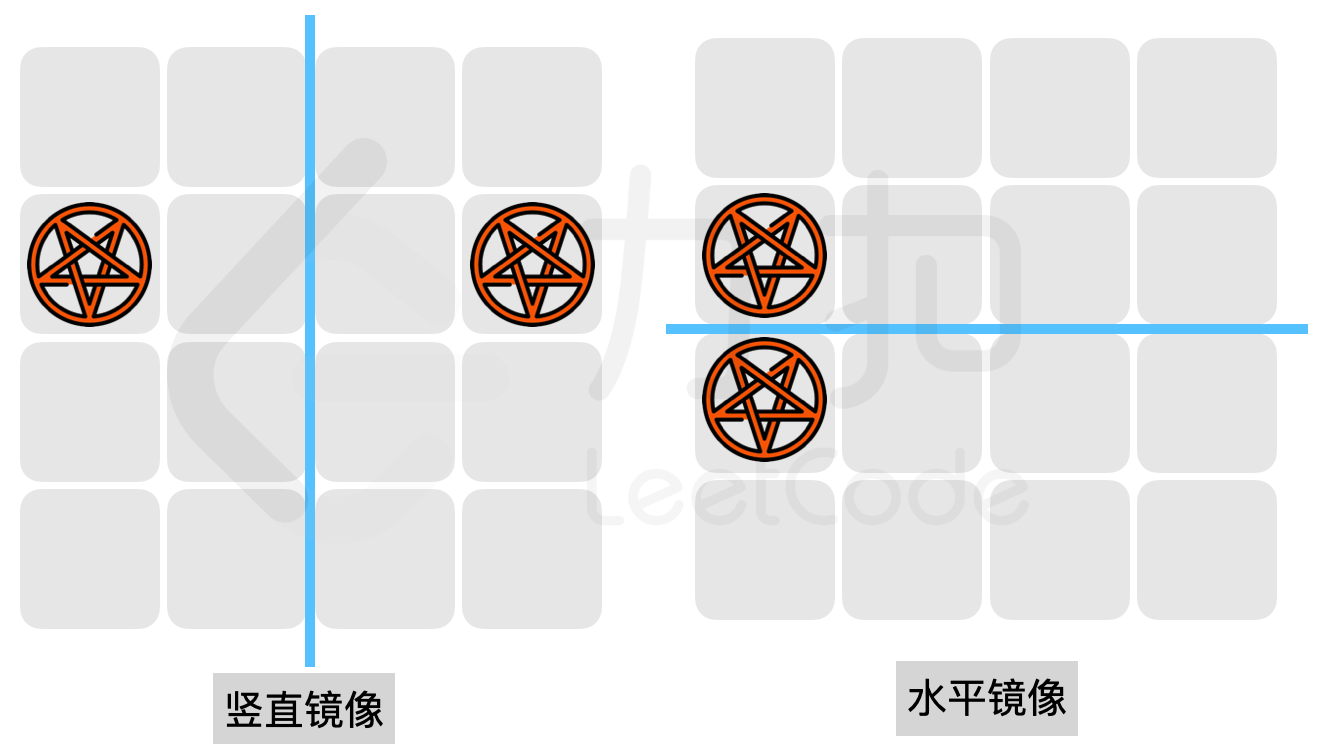{:width=400px}
|
||||
|
||||
在使用卷轴后,小扣将被「附加负面效果」,因此小扣需要尽可能缩短传送后到达魔法水晶的距离。而守护者的目标是阻止小扣到达魔法水晶的位置;如果无法阻止,则尽可能 **增加** 小扣传送后到达魔法水晶的距离。
|
||||
假设小扣和守护者都按最优策略行事,返回小扣需要在 「附加负面效果」的情况下 **最少** 移动多少次才能到达魔法水晶。如果无法到达,返回 `-1`。
|
||||
|
||||
**注意:**
|
||||
- 守护者可以不使用卷轴;
|
||||
- 传送后的镜像位置可能与原位置相同。
|
||||
|
||||
**示例 1:**
|
||||
>输入:`maze = [".....","##S..","...#.","T.#..","###.."]`
|
||||
>
|
||||
>输出:`7`
|
||||
>
|
||||
>解释:如下图所示:
|
||||
>守护者释放魔法的两个最佳的位置为 [2,0] 或 [3,1]:
|
||||
>若小扣经过 [2,0],守护者在该位置释放魔法,
|
||||
>小扣被传送至 [2,4] 处且加上负面效果,此时小扣还需要移动 7 次才能到达魔法水晶;
|
||||
>若小扣经过 [3,1],守护者在该位置释放魔法,
|
||||
>小扣被传送至 [3,3] 处且加上负面效果,此时小扣还需要移动 9 次才能到达魔法水晶;
|
||||
>因此小扣负面效果下最少需要移动 7 次才能到达魔法水晶。
|
||||
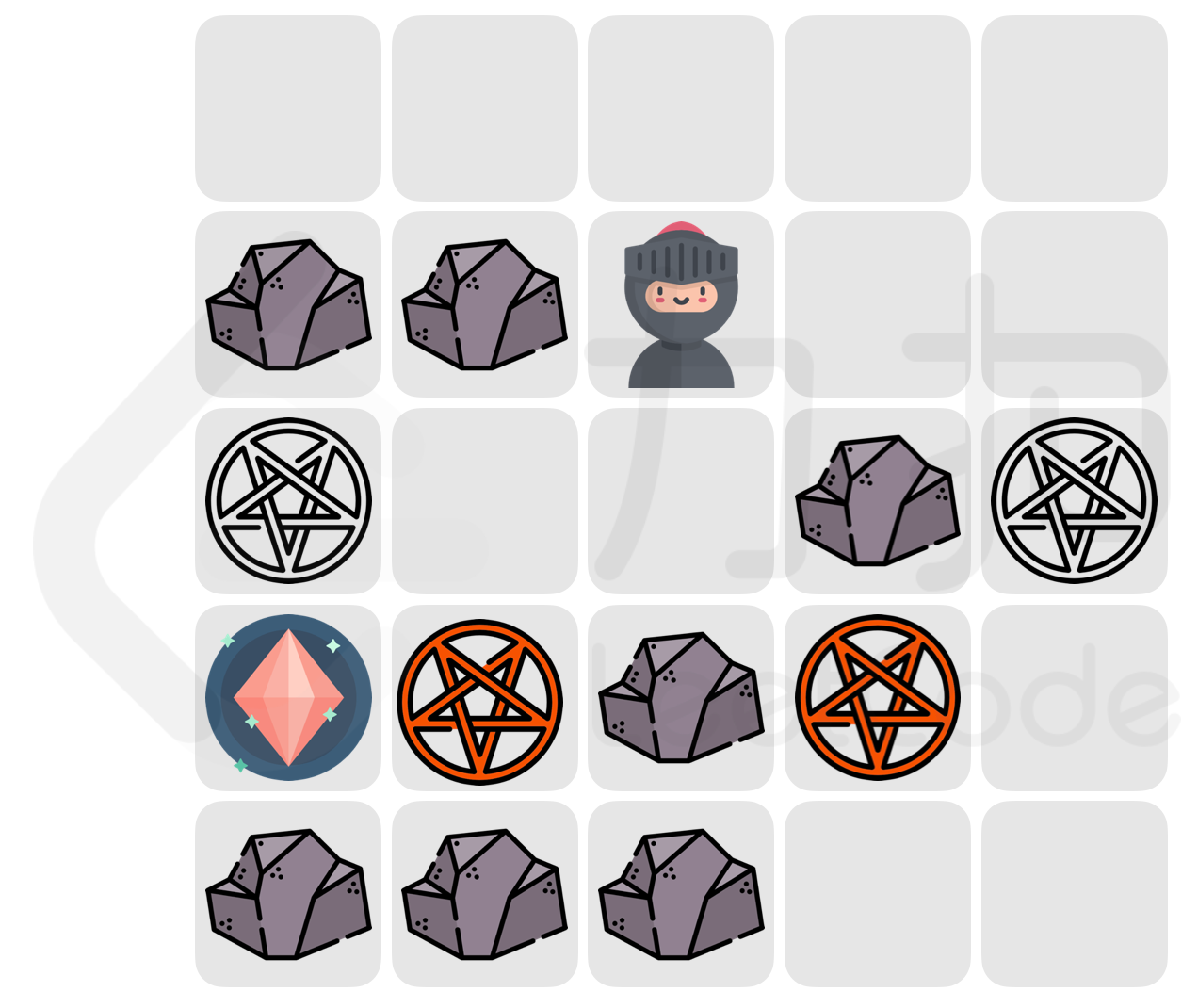{:width=300px}
|
||||
|
||||
|
||||
**示例 2:**
|
||||
>输入:`maze = [".#..","..##",".#S.",".#.T"]`
|
||||
>
|
||||
>输出:`-1`
|
||||
>
|
||||
>解释:如下图所示。
|
||||
>若小扣向下移动至 [3,2],守护者使其传送至 [0,2],小扣将无法到达魔法水晶;
|
||||
>若小扣向右移动至 [2,3],守护者使其传送至 [2,0],小扣将无法到达魔法水晶;
|
||||
{:width=300px}
|
||||
|
||||
|
||||
**示例 3:**
|
||||
>输入:`maze = ["S###.","..###","#..##","##..#","###.T"]`
|
||||
>
|
||||
>输出:`5`
|
||||
>
|
||||
>解释:如下图所示:
|
||||
>守护者需要小扣在空地才能释放,因此初始无法将其从 [0,0] 传送至 [0,4];
|
||||
>当小扣移动至 [2,1] 时,释放卷轴将其传送至水平方向的镜像位置 [2,1](为原位置)
|
||||
>而后小扣需要移动 5 次到达魔法水晶
|
||||
{:width=300px}
|
||||
|
||||
**提示:**
|
||||
- `4 <= maze.length == maze[i].length <= 200`
|
||||
- `maze[i][j]` 仅包含 `"."`、`"#"`、`"S"`、`"T"`
|
||||
@@ -0,0 +1,38 @@
|
||||
<p>给你一个下标从 <strong>0</strong> 开始的 <strong>正</strong> 整数数组 <code>nums</code> 。你可以对数组执行以下操作 <strong>任意</strong> 次:</p>
|
||||
|
||||
<ul>
|
||||
<li>选择一个满足 <code>0 <= i < n - 1</code> 的下标 <code>i</code> ,将 <code>nums[i]</code> 或者 <code>nums[i+1]</code> 两者之一替换成它们的最大公约数。</li>
|
||||
</ul>
|
||||
|
||||
<p>请你返回使数组 <code>nums</code> 中所有元素都等于 <code>1</code> 的 <strong>最少</strong> 操作次数。如果无法让数组全部变成 <code>1</code> ,请你返回 <code>-1</code> 。</p>
|
||||
|
||||
<p>两个正整数的最大公约数指的是能整除这两个数的最大正整数。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre><b>输入:</b>nums = [2,6,3,4]
|
||||
<b>输出:</b>4
|
||||
<b>解释:</b>我们可以执行以下操作:
|
||||
- 选择下标 i = 2 ,将 nums[2] 替换为 gcd(3,4) = 1 ,得到 nums = [2,6,1,4] 。
|
||||
- 选择下标 i = 1 ,将 nums[1] 替换为 gcd(6,1) = 1 ,得到 nums = [2,1,1,4] 。
|
||||
- 选择下标 i = 0 ,将 nums[0] 替换为 gcd(2,1) = 1 ,得到 nums = [1,1,1,4] 。
|
||||
- 选择下标 i = 2 ,将 nums[3] 替换为 gcd(1,4) = 1 ,得到 nums = [1,1,1,1] 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre><b>输入:</b>nums = [2,10,6,14]
|
||||
<b>输出:</b>-1
|
||||
<b>解释:</b>无法将所有元素都变成 1 。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>2 <= nums.length <= 50</code></li>
|
||||
<li><code>1 <= nums[i] <= 10<sup>6</sup></code></li>
|
||||
</ul>
|
||||
34
leetcode-cn/problem (Chinese)/倍数求和 [sum-multiples].html
Normal file
34
leetcode-cn/problem (Chinese)/倍数求和 [sum-multiples].html
Normal file
@@ -0,0 +1,34 @@
|
||||
<p>给你一个正整数 <code>n</code> ,请你计算在 <code>[1,n]</code> 范围内能被 <code>3</code>、<code>5</code>、<code>7</code> 整除的所有整数之和。</p>
|
||||
|
||||
<p>返回一个整数,用于表示给定范围内所有满足约束条件的数字之和。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre><strong>输入:</strong>n = 7
|
||||
<strong>输出:</strong>21
|
||||
<strong>解释:</strong>在 <code>[1, 7]</code> 范围内能被 3、<code>5、</code><code>7 整除的所有整数分别是</code><code> 3、5、6、7</code> 。数字之和为 <code>21</code> 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre><strong>输入:</strong>n = 10
|
||||
<strong>输出:</strong>40
|
||||
<strong>解释:</strong>在 <code>[1, 10]</code> 范围内能被 3、<code>5、</code><code>7 整除的所有整数分别是</code><code> 3、5、6、7、9、10</code> 。数字之和为 <code>40</code> 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 3:</strong></p>
|
||||
|
||||
<pre><strong>输入:</strong>n = 9
|
||||
<strong>输出:</strong>30
|
||||
<strong>解释:</strong>在 <code>[1, 9]</code> 范围内能被 3、<code>5、</code><code>7 整除的所有整数分别是</code><code> 3、5、6、7、9</code> 。数字之和为 <code>30</code> 。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= n <= 10<sup>3</sup></code></li>
|
||||
</ul>
|
||||
79
leetcode-cn/problem (Chinese)/函数防抖 [debounce].html
Normal file
79
leetcode-cn/problem (Chinese)/函数防抖 [debounce].html
Normal file
@@ -0,0 +1,79 @@
|
||||
<p>请你编写一个函数,接收参数为另一个函数和一个以毫秒为单位的时间 <code>t</code> ,并返回该函数的 <b>函数防抖 </b>后的结果。</p>
|
||||
|
||||
<p><b>函数防抖 </b>方法是一个函数,它的执行被延迟了 <code>t</code> 毫秒,如果在这个时间窗口内再次调用它,它的执行将被取消。你编写的防抖函数也应该接收传递的参数。</p>
|
||||
|
||||
<p>例如,假设 <code>t = 50ms</code> ,函数分别在 <code>30ms</code> 、 <code>60ms</code> 和 <code>100ms</code> 时调用。前两个函数调用将被取消,第三个函数调用将在 <code>150ms</code> 执行。如果改为 <code>t = 35ms</code> ,则第一个调用将被取消,第二个调用将在 <code>95ms</code> 执行,第三个调用将在 <code>135ms</code> 执行。</p>
|
||||
|
||||
<p><img alt="Debounce Schematic" src="https://assets.leetcode.com/uploads/2023/04/08/screen-shot-2023-04-08-at-11048-pm.png" style="width: 800px; height: 242px;" /></p>
|
||||
|
||||
<p>上图展示了了防抖函数是如何转换事件的。其中,每个矩形表示 100ms,反弹时间为 400ms。每种颜色代表一组不同的输入。</p>
|
||||
|
||||
<p>请在不使用 lodash 的 <code>_.debounce()</code> 函数的前提下解决该问题。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong class="example">示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
t = 50
|
||||
calls = [
|
||||
{"t": 50, inputs: [1]},
|
||||
{"t": 75, inputs: [2]}
|
||||
]
|
||||
<b>输出:</b>[{"t": 125, inputs: [2]}]
|
||||
<strong>解释:</strong>
|
||||
let start = Date.now();
|
||||
function log(...inputs) {
|
||||
console.log([Date.now() - start, inputs ])
|
||||
}
|
||||
const dlog = debounce(log, 50);
|
||||
setTimeout(() => dlog(1), 50);
|
||||
setTimeout(() => dlog(2), 75);
|
||||
|
||||
第一次调用被第二次调用取消,因为第二次调用发生在 100ms 之前
|
||||
第二次调用延迟 50ms,在 125ms 执行。输入为 (2)。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
t = 20
|
||||
calls = [
|
||||
{"t": 50, inputs: [1]},
|
||||
{"t": 100, inputs: [2]}
|
||||
]
|
||||
<b>输出:</b>[{"t": 70, inputs: [1]}, {"t": 120, inputs: [2]}]
|
||||
<strong>解释:</strong>
|
||||
第一次调用延迟到 70ms。输入为 (1)。
|
||||
第二次调用延迟到 120ms。输入为 (2)。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
t = 150
|
||||
calls = [
|
||||
{"t": 50, inputs: [1, 2]},
|
||||
{"t": 300, inputs: [3, 4]},
|
||||
{"t": 300, inputs: [5, 6]}
|
||||
]
|
||||
<b>输出:</b>[{"t": 200, inputs: [1,2]}, {"t": 450, inputs: [5, 6]}]
|
||||
<strong>解释:</strong>
|
||||
第一次调用延迟了 150ms,运行时间为 200ms。输入为 (1, 2)。
|
||||
第二次调用被第三次调用取消
|
||||
第三次调用延迟了 150ms,运行时间为 450ms。输入为 (5, 6)。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>0 <= t <= 1000</code></li>
|
||||
<li><code>1 <= calls.length <= 10</code></li>
|
||||
<li><code>0 <= calls[i].t <= 1000</code></li>
|
||||
<li><code>0 <= calls[i].inputs.length <= 10</code></li>
|
||||
</ul>
|
||||
85
leetcode-cn/problem (Chinese)/分组 [group-by].html
Normal file
85
leetcode-cn/problem (Chinese)/分组 [group-by].html
Normal file
@@ -0,0 +1,85 @@
|
||||
<p>请你编写一段可应用于所有数组的代码,使任何数组调用 <code>array. groupBy(fn)</code> 方法时,它返回对该数组 <strong>分组后</strong> 的结果。</p>
|
||||
|
||||
<p>数组 <strong>分组</strong> 是一个对象,其中的每个键都是 <code>fn(arr[i])</code> 的输出的一个数组,该数组中含有原数组中具有该键的所有项。</p>
|
||||
|
||||
<p>提供的回调函数 <code>fn</code> 将接受数组中的项并返回一个字符串类型的键。</p>
|
||||
|
||||
<p>每个值列表的顺序应该与元素在数组中出现的顺序相同。任何顺序的键都是可以接受的。</p>
|
||||
|
||||
<p>请在不使用 lodash 的 <code>_.groupBy</code> 函数的前提下解决这个问题。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
array = [
|
||||
{"id":"1"},
|
||||
{"id":"1"},
|
||||
{"id":"2"}
|
||||
],
|
||||
fn = function (item) {
|
||||
return item.id;
|
||||
}
|
||||
<b>输出:</b>
|
||||
{
|
||||
"1": [{"id": "1"}, {"id": "1"}],
|
||||
"2": [{"id": "2"}]
|
||||
}
|
||||
<strong>解释:</strong>
|
||||
输出来自函数 array.groupBy(fn)。
|
||||
分组选择方法是从数组中的每个项中获取 "id" 。
|
||||
有两个 "id" 为 1 的对象。所以将这两个对象都放在第一个数组中。
|
||||
有一个 "id" 为 2 的对象。所以该对象被放到第二个数组中。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
array = [
|
||||
[1, 2, 3],
|
||||
[1, 3, 5],
|
||||
[1, 5, 9]
|
||||
]
|
||||
fn = function (list) {
|
||||
return String(list[0]);
|
||||
}
|
||||
<b>输出:</b>
|
||||
{
|
||||
"1": [[1, 2, 3], [1, 3, 5], [1, 5, 9]]
|
||||
}
|
||||
<strong>解释:</strong>
|
||||
数组可以是任何类型的。在本例中,分组选择方法是将键定义为数组中的第一个元素。
|
||||
所有数组的第一个元素都是1,所以它们被组合在一起。
|
||||
{
|
||||
"1": [[1, 2, 3], [1, 3, 5], [1, 5, 9]]
|
||||
}
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输出:</b>
|
||||
array = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
|
||||
fn = function (n) {
|
||||
return String(n > 5);
|
||||
}
|
||||
<strong>输入:</strong>
|
||||
{
|
||||
"true": [6, 7, 8, 9, 10],
|
||||
"false": [1, 2, 3, 4, 5]
|
||||
}
|
||||
<strong>解释:</strong>
|
||||
分组选择方法是根据每个数字是否大于 5 来分割数组。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>0 <= array.length <= 10<sup>5</sup></code></li>
|
||||
<li><code>fn 返回一个字符串</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,52 @@
|
||||
<p>请你编写一个函数,它接收一个函数数组 <code>[f1, f2, f3,…], fn]</code> ,并返回一个新的函数 <code>fn</code> ,它是函数数组的 <strong>复合函数</strong> 。</p>
|
||||
|
||||
<p><code>[f(x), g(x), h(x)]</code> 的 <strong>复合函数</strong> 为 <code>fn(x) = f(g(h(x)))</code> 。</p>
|
||||
|
||||
<p>一个空函数列表的 <strong>复合函数</strong> 是 <strong>恒等函数</strong> <code>f(x) = x</code> 。</p>
|
||||
|
||||
<p>你可以假设数组中的每个函数接受一个整型参数作为输入,并返回一个整型作为输出。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong class="example">示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>functions = [x => x + 1, x => x * x, x => 2 * x], x = 4
|
||||
<b>输出:</b>65
|
||||
<strong>解释:</strong>
|
||||
从右向左计算......
|
||||
Starting with x = 4.
|
||||
2 * (4) = 8
|
||||
(8) * (8) = 64
|
||||
(64) + 1 = 65
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输出:</b>functions = [x => 10 * x, x => 10 * x, x => 10 * x], x = 1
|
||||
<b>输入:</b>1000
|
||||
<strong>解释:</strong>
|
||||
从右向左计算......
|
||||
10 * (1) = 10
|
||||
10 * (10) = 100
|
||||
10 * (100) = 1000
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>functions = [], x = 42
|
||||
<b>输出:</b>42
|
||||
<strong>解释:</strong>
|
||||
空函数列表的复合函数就是恒等函数</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code><font face="monospace">-1000 <= x <= 1000</font></code></li>
|
||||
<li><code><font face="monospace">0 <= functions.length <= 1000</font></code></li>
|
||||
<li><font face="monospace"><code>所有函数都接受并返回一个整型</code></font></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,50 @@
|
||||
<p>给定两个对象 <code>o1</code> 和 <code>o2</code> ,请你检查它们是否 <strong>完全相等</strong> 。</p>
|
||||
|
||||
<p>对于两个 <strong>完全相等</strong> 的对象,它们必须包含相同的键,并且相关的值也必须 <strong>完全相等</strong> 。如果两个对象通过了 <code>===</code> 相等性检查,它们也被认为是 <strong>完全相等</strong> 的。</p>
|
||||
|
||||
<p>你可以假设这两个对象都是 <code>JSON.parse</code> 的输出。换句话说,它们是有效的 <code>JSON</code> 。</p>
|
||||
|
||||
<p>请你在不使用 lodash 的 <code>_.isEqual()</code> 函数的前提下解决这个问题。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>o1 = {"x":1,"y":2}, o2 = {"x":1,"y":2}
|
||||
<b>输出:</b>true
|
||||
<b>输入:</b>键和值完全匹配。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>o1 = {"y":2,"x":1}, o2 = {"x":1,"y":2}
|
||||
<b>输出:</b>true
|
||||
<b>解释:</b>尽管键的顺序不同,但它们仍然完全匹配。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>o1 = {"x":null,"L":[1,2,3]}, o2 = {"x":null,"L":["1","2","3"]}
|
||||
<b>输出:</b>false
|
||||
<b>解释:</b>数字数组不同于字符串数组。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 4:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>o1 = true, o2 = false
|
||||
<b>输出:</b>false
|
||||
<b>解释:</b>true !== false</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= JSON.stringify(o1).length <= 10<sup>5</sup></code></li>
|
||||
<li><code>1 <= JSON.stringify(o2).length <= 10<sup>5</sup></code></li>
|
||||
<li><code>maxNestingDepth <= 1000</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,50 @@
|
||||
<p>现给定一个对象,返回该对象的有效 JSON 字符串。你可以假设这个对象只包括字符串、整数、数组、对象、布尔值和 null。返回的字符串不能包含额外的空格。键的返回顺序应该与 <code>Object.keys()</code> 的顺序相同。</p>
|
||||
|
||||
<p>请你在不使用内置方法 <code>JSON.stringify</code> 的前提下解决这个问题。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>object = {"y":1,"x":2}
|
||||
<b>输出:</b>{"y":1,"x":2}
|
||||
<b>解释:</b>
|
||||
返回该对象的 JSON 表示形式。
|
||||
注意,键的返回顺序应该与 Object.keys() 的顺序相同。</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>object = {"a":"str","b":-12,"c":true,"d":null}
|
||||
<b>输出:</b>{"a":"str","b":-12,"c":true,"d":null}
|
||||
<strong>解释:</strong>
|
||||
JSON 的基本类型是字符串、数字型、布尔值和 null。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>object = {"key":{"a":1,"b":[{},null,"Hello"]}}
|
||||
<b>输出:</b>{"key":{"a":1,"b":[{},null,"Hello"]}}
|
||||
<b>解释:</b>
|
||||
对象和数组可以包括其他对象和数组。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 4:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>object = true
|
||||
<b>输出:</b>true
|
||||
<b>解释:</b>
|
||||
基本类型是有效的输入</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>Constraints:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>对象包括字符串、整数、布尔值、数组、对象和 null</code></li>
|
||||
<li><code>1 <= JSON.stringify(object).length <= 10<sup>5</sup></code></li>
|
||||
<li><code>maxNestingLevel <= 1000</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,38 @@
|
||||
<p>现给定一个整数的 <strong>多维数组</strong> ,请你返回一个生成器对象,按照 <strong>中序遍历</strong> 的顺序逐个生成整数。</p>
|
||||
|
||||
<p><strong>多维数组</strong> 是一个递归数据结构,包含整数和其他 <strong>多维数组</strong>。</p>
|
||||
|
||||
<p><strong>中序遍历</strong> 是从左到右遍历每个数组,在遇到任何整数时生成它,遇到任何数组时递归应用 <strong>中序遍历</strong> 。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>arr = [[[6]],[1,3],[]]
|
||||
<b>输出:</b>[6,1,3]
|
||||
<strong>解释:</strong>
|
||||
const generator = inorderTraversal(arr);
|
||||
generator.next().value; // 6
|
||||
generator.next().value; // 1
|
||||
generator.next().value; // 3
|
||||
generator.next().done; // true
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>arr = []
|
||||
<b>输出:</b>[]
|
||||
<b>解释:</b>输入的多维数组没有任何参数,所以生成器不需要生成任何值。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>0 <= arr.flat().length <= 10<sup>5</sup></code></li>
|
||||
<li><code>0 <= arr.flat()[i] <= 10<sup>5</sup></code></li>
|
||||
<li><code>maxNestingDepth <= 10<sup>5</sup></code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,51 @@
|
||||
<p>给你两个下标从 <strong>0</strong> 开始的整数数组 <code>nums</code> 和 <code>divisors</code> 。</p>
|
||||
|
||||
<p><code>divisors[i]</code> 的 <strong>可整除性得分</strong> 等于满足 <code>nums[j]</code> 能被 <code>divisors[i]</code> 整除的下标 <code>j</code> 的数量。</p>
|
||||
|
||||
<p>返回 <strong>可整除性得分</strong> 最大的整数 <code>divisors[i]</code> 。如果有多个整数具有最大得分,则返回数值最小的一个。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>nums = [4,7,9,3,9], divisors = [5,2,3]
|
||||
<strong>输出:</strong>3
|
||||
<strong>解释:</strong>divisors 中每个元素的可整除性得分为:
|
||||
divisors[0] 的可整除性得分为 0 ,因为 nums 中没有任何数字能被 5 整除。
|
||||
divisors[1] 的可整除性得分为 1 ,因为 nums[0] 能被 2 整除。
|
||||
divisors[2] 的可整除性得分为 3 ,因为 nums[2]、nums[3] 和 nums[4] 都能被 3 整除。
|
||||
因此,返回 divisors[2] ,它的可整除性得分最大。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>nums = [20,14,21,10], divisors = [5,7,5]
|
||||
<strong>输出:</strong>5
|
||||
<strong>解释:</strong>divisors 中每个元素的可整除性得分为:
|
||||
divisors[0] 的可整除性得分为 2 ,因为 nums[0] 和 nums[3] 都能被 5 整除。
|
||||
divisors[1] 的可整除性得分为 2 ,因为 nums[1] 和 nums[2] 都能被 7 整除。
|
||||
divisors[2] 的可整除性得分为 2 ,因为 nums[0] 和 nums[3] 都能被5整除。
|
||||
由于 divisors[0]、divisors[1] 和 divisors[2] 的可整除性得分都是最大的,因此,我们返回数值最小的一个,即 divisors[2] 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>nums = [12], divisors = [10,16]
|
||||
<strong>输出:</strong>10
|
||||
<strong>解释:</strong>divisors 中每个元素的可整除性得分为:
|
||||
divisors[0] 的可整除性得分为 0 ,因为 nums 中没有任何数字能被 10 整除。
|
||||
divisors[1] 的可整除性得分为 0 ,因为 nums 中没有任何数字能被 16 整除。
|
||||
由于 divisors[0] 和 divisors[1] 的可整除性得分都是最大的,因此,我们返回数值最小的一个,即 divisors[0] 。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= nums.length, divisors.length <= 1000</code></li>
|
||||
<li><code>1 <= nums[i], divisors[i] <= 10<sup>9</sup></code></li>
|
||||
</ul>
|
||||
50
leetcode-cn/problem (Chinese)/探险营地 [0Zeoeg].md
Normal file
50
leetcode-cn/problem (Chinese)/探险营地 [0Zeoeg].md
Normal file
@@ -0,0 +1,50 @@
|
||||
探险家小扣的行动轨迹,都将保存在记录仪中。`expeditions[i]` 表示小扣第 `i` 次探险记录,用一个字符串数组表示。其中的每个「营地」由大小写字母组成,通过子串 `->` 连接。
|
||||
> 例:"Leet->code->Campsite",表示到访了 "Leet"、"code"、"Campsite" 三个营地。
|
||||
|
||||
`expeditions[0]` 包含了初始小扣已知的所有营地;对于之后的第 `i` 次探险(即 `expeditions[i]` 且 i > 0),如果记录中包含了之前均没出现的营地,则表示小扣 **新发现** 的营地。
|
||||
|
||||
请你找出小扣发现新营地最多且索引最小的那次探险,并返回对应的记录索引。如果所有探险记录都没有发现新的营地,返回 `-1`
|
||||
|
||||
**注意:**
|
||||
- 大小写不同的营地视为不同的营地;
|
||||
- 营地的名称长度均大于 `0`。
|
||||
|
||||
**示例 1:**
|
||||
>输入:`expeditions = ["leet->code","leet->code->Campsite->Leet","leet->code->leet->courier"]`
|
||||
>
|
||||
>输出:`1`
|
||||
>
|
||||
>解释:
|
||||
>初始已知的所有营地为 "leet" 和 "code"
|
||||
>第 1 次,到访了 "leet"、"code"、"Campsite"、"Leet",新发现营地 2 处:"Campsite"、"Leet"
|
||||
>第 2 次,到访了 "leet"、"code"、"courier",新发现营地 1 处:"courier"
|
||||
>第 1 次探险发现的新营地数量最多,因此返回 `1`
|
||||
|
||||
**示例 2:**
|
||||
>输入:`expeditions = ["Alice->Dex","","Dex"]`
|
||||
>
|
||||
>输出:`-1`
|
||||
>
|
||||
>解释:
|
||||
>初始已知的所有营地为 "Alice" 和 "Dex"
|
||||
>第 1 次,未到访任何营地;
|
||||
>第 2 次,到访了 "Dex",未新发现营地;
|
||||
>因为两次探险均未发现新的营地,返回 `-1`
|
||||
|
||||
**示例 3:**
|
||||
>输入:`expeditions = ["","Gryffindor->Slytherin->Gryffindor","Hogwarts->Hufflepuff->Ravenclaw"]`
|
||||
>
|
||||
>输出:`2`
|
||||
>
|
||||
>解释:
|
||||
>初始未发现任何营地;
|
||||
>第 1 次,到访 "Gryffindor"、"Slytherin" 营地,其中重复到访 "Gryffindor" 两次,
|
||||
>因此新发现营地为 2 处:"Gryffindor"、"Slytherin"
|
||||
>第 2 次,到访 "Hogwarts"、"Hufflepuff"、"Ravenclaw" 营地;
|
||||
>新发现营地 3 处:"Hogwarts"、"Hufflepuff"、"Ravenclaw";
|
||||
>第 2 次探险发现的新营地数量最多,因此返回 `2`
|
||||
|
||||
**提示:**
|
||||
- `1 <= expeditions.length <= 1000`
|
||||
- `0 <= expeditions[i].length <= 1000`
|
||||
- 探险记录中只包含大小写字母和子串"->"
|
||||
@@ -0,0 +1,28 @@
|
||||
<p>请你编写一段代码实现一个数组方法,使任何数组都可以调用 <code>array.last()</code> 方法,这个方法将返回数组最后一个元素。如果数组中没有元素,则返回 <code>-1</code> 。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1 :</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>nums = [1,2,3]
|
||||
<b>输出:</b>3
|
||||
<b>解释</b>:调用 nums.last() 后返回最后一个元素: 3。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2 :</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>nums = []
|
||||
<b>输出:</b>-1
|
||||
<strong>解释:</strong>因为此数组没有元素,所以应该返回 -1。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><b>提示:</b></p>
|
||||
|
||||
<ul>
|
||||
<li><code>0 <= arr.length <= 1000</code></li>
|
||||
<li><code>0 <= arr[i] <= 1000</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,64 @@
|
||||
<p>请你编写一个函数,它的参数为一个整数数组 <code>nums</code> 、一个计算函数 <code>fn</code> 和初始值 <font color="#c7254e"><font face="Menlo, Monaco, Consolas, Courier New, monospace"><span style="font-size:12.6px"><span style="background-color:#f9f2f4">init </span></span></font></font>。返回一个数组 <strong>归约后 </strong>的值。</p>
|
||||
|
||||
<p>你可以定义一个数组 <strong>归约后 </strong>的值,然后应用以下操作: <code>val = fn(init, nums[0])</code> , <code>val = fn(val, nums[1])</code> , <code>val = fn(val, arr[2])</code> ,<code>...</code> 直到数组中的每个元素都被处理完毕。返回 <code>val</code> 的最终值。</p>
|
||||
|
||||
<p>如果数组的长度为 0,它应该返回 <code>init</code> 的值。</p>
|
||||
|
||||
<p>请你在不使用内置数组方法的 <code>Array.reduce</code> 前提下解决这个问题。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong class="example">示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>
|
||||
nums = [1,2,3,4]
|
||||
fn = function sum(accum, curr) { return accum + curr; }
|
||||
init = 0
|
||||
<strong>输出:</strong>10
|
||||
<strong>解释:</strong>
|
||||
初始值为 init=0 。
|
||||
(0) + nums[0] = 1
|
||||
(1) + nums[1] = 3
|
||||
(3) + nums[2] = 6
|
||||
(6) + nums[3] = 10
|
||||
Val 最终值为 10。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>
|
||||
nums = [1,2,3,4]
|
||||
fn = function sum(accum, curr) { return accum + curr * curr; }
|
||||
init = 100
|
||||
<strong>输出:</strong>130
|
||||
<strong>解释:</strong>
|
||||
初始值为 init=0 。
|
||||
(100) + nums[0]^2 = 101
|
||||
(101) + nums[1]^2 = 105
|
||||
(105) + nums[2]^2 = 114
|
||||
(114) + nums[3]^2 = 130
|
||||
Val 最终值为 130。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>
|
||||
nums = []
|
||||
fn = function sum(accum, curr) { return 0; }
|
||||
init = 25
|
||||
<strong>输出:</strong>25
|
||||
<b>解释:</b>这是一个空数组,所以返回 init 。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>0 <= nums.length <= 1000</code></li>
|
||||
<li><code>0 <= nums[i] <= 1000</code></li>
|
||||
<li><code>0 <= init <= 1000</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,50 @@
|
||||
<p>现有一棵无向、无根的树,树中有 <code>n</code> 个节点,按从 <code>0</code> 到 <code>n - 1</code> 编号。给你一个整数 <code>n</code> 和一个长度为 <code>n - 1</code> 的二维整数数组 <code>edges</code> ,其中 <code>edges[i] = [a<sub>i</sub>, b<sub>i</sub>]</code> 表示树中节点 <code>a<sub>i</sub></code> 和 <code>b<sub>i</sub></code> 之间存在一条边。</p>
|
||||
|
||||
<p>每个节点都关联一个价格。给你一个整数数组 <code>price</code> ,其中 <code>price[i]</code> 是第 <code>i</code> 个节点的价格。</p>
|
||||
|
||||
<p>给定路径的 <strong>价格总和</strong> 是该路径上所有节点的价格之和。</p>
|
||||
|
||||
<p>另给你一个二维整数数组 <code>trips</code> ,其中 <code>trips[i] = [start<sub>i</sub>, end<sub>i</sub>]</code> 表示您从节点 <code>start<sub>i</sub></code> 开始第 <code>i</code> 次旅行,并通过任何你喜欢的路径前往节点 <code>end<sub>i</sub></code> 。</p>
|
||||
|
||||
<p>在执行第一次旅行之前,你可以选择一些 <strong>非相邻节点</strong> 并将价格减半。</p>
|
||||
|
||||
<p>返回执行所有旅行的最小价格总和。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
<img alt="" src="https://assets.leetcode.com/uploads/2023/03/16/diagram2.png" style="width: 541px; height: 181px;">
|
||||
<pre><strong>输入:</strong>n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
|
||||
<strong>输出:</strong>23
|
||||
<strong>解释:
|
||||
</strong>上图表示将节点 2 视为根之后的树结构。第一个图表示初始树,第二个图表示选择节点 0 、2 和 3 并使其价格减半后的树。
|
||||
第 1 次旅行,选择路径 [0,1,3] 。路径的价格总和为 1 + 2 + 3 = 6 。
|
||||
第 2 次旅行,选择路径 [2,1] 。路径的价格总和为 2 + 5 = 7 。
|
||||
第 3 次旅行,选择路径 [2,1,3] 。路径的价格总和为 5 + 2 + 3 = 10 。
|
||||
所有旅行的价格总和为 6 + 7 + 10 = 23 。可以证明,23 是可以实现的最小答案。</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
<img alt="" src="https://assets.leetcode.com/uploads/2023/03/16/diagram3.png" style="width: 456px; height: 111px;">
|
||||
<pre><strong>输入:</strong>n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
|
||||
<strong>输出:</strong>1
|
||||
<strong>解释:</strong>
|
||||
上图表示将节点 0 视为根之后的树结构。第一个图表示初始树,第二个图表示选择节点 0 并使其价格减半后的树。
|
||||
第 1 次旅行,选择路径 [0] 。路径的价格总和为 1 。
|
||||
所有旅行的价格总和为 1 。可以证明,1 是可以实现的最小答案。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= n <= 50</code></li>
|
||||
<li><code>edges.length == n - 1</code></li>
|
||||
<li><code>0 <= a<sub>i</sub>, b<sub>i</sub> <= n - 1</code></li>
|
||||
<li><code>edges</code> 表示一棵有效的树</li>
|
||||
<li><code>price.length == n</code></li>
|
||||
<li><code>price[i]</code> 是一个偶数</li>
|
||||
<li><code>1 <= price[i] <= 1000</code></li>
|
||||
<li><code>1 <= trips.length <= 100</code></li>
|
||||
<li><code>0 <= start<sub>i</sub>, end<sub>i</sub> <= n - 1</code></li>
|
||||
</ul>
|
||||
35
leetcode-cn/problem (Chinese)/最强祝福力场 [xepqZ5].md
Normal file
35
leetcode-cn/problem (Chinese)/最强祝福力场 [xepqZ5].md
Normal file
@@ -0,0 +1,35 @@
|
||||
小扣在探索丛林的过程中,无意间发现了传说中“落寞的黄金之都”。而在这片建筑废墟的地带中,小扣使用探测仪监测到了存在某种带有「祝福」效果的力场。
|
||||
经过不断的勘测记录,小扣将所有力场的分布都记录了下来。`forceField[i] = [x,y,side]` 表示第 `i` 片力场将覆盖以坐标 `(x,y)` 为中心,边长为 `side` 的正方形区域。
|
||||
|
||||
若任意一点的 **力场强度** 等于覆盖该点的力场数量,请求出在这片地带中 **力场强度** 最强处的 **力场强度**。
|
||||
|
||||
**注意:**
|
||||
- 力场范围的边缘同样被力场覆盖。
|
||||
|
||||
**示例 1:**
|
||||
>输入:
|
||||
>`forceField = [[0,0,1],[1,0,1]]`
|
||||
>
|
||||
>输出:`2`
|
||||
>
|
||||
>解释:如图所示,(0.5, 0) 处力场强度最强为 2, (0.5,-0.5)处力场强度同样是 2。
|
||||
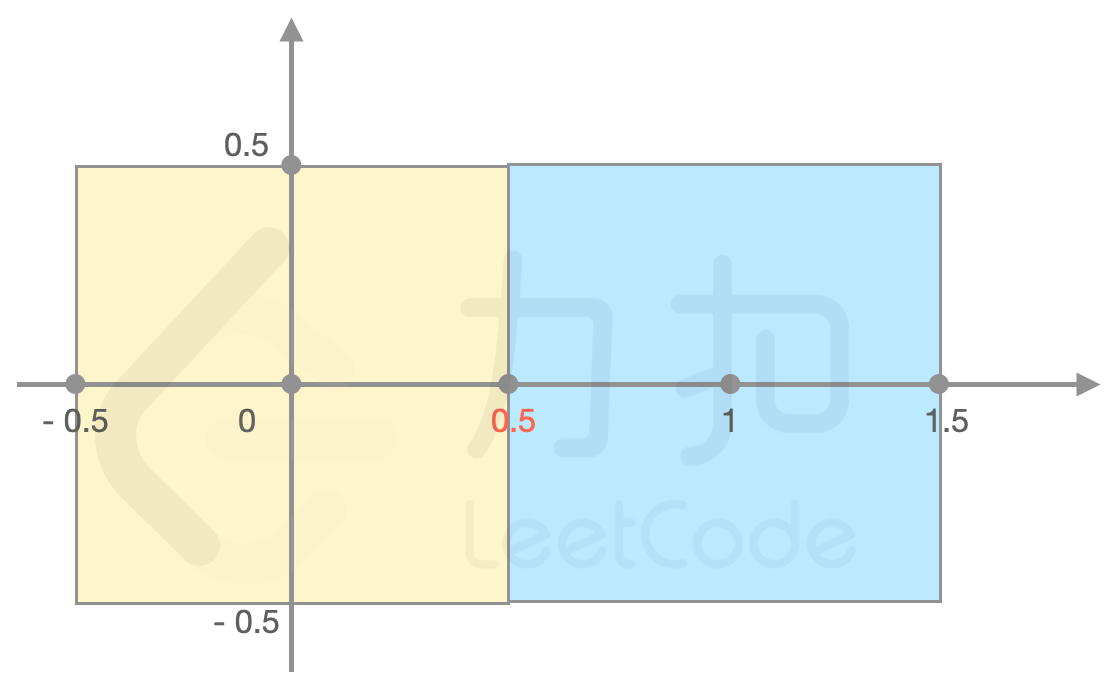{:width=400px}
|
||||
|
||||
|
||||
**示例 2:**
|
||||
>输入:
|
||||
>`forceField = [[4,4,6],[7,5,3],[1,6,2],[5,6,3]]`
|
||||
>
|
||||
>输出:`3`
|
||||
>
|
||||
>解释:如下图所示,
|
||||
>`forceField[0]、forceField[1]、forceField[3]` 重叠的区域力场强度最大,返回 `3`
|
||||
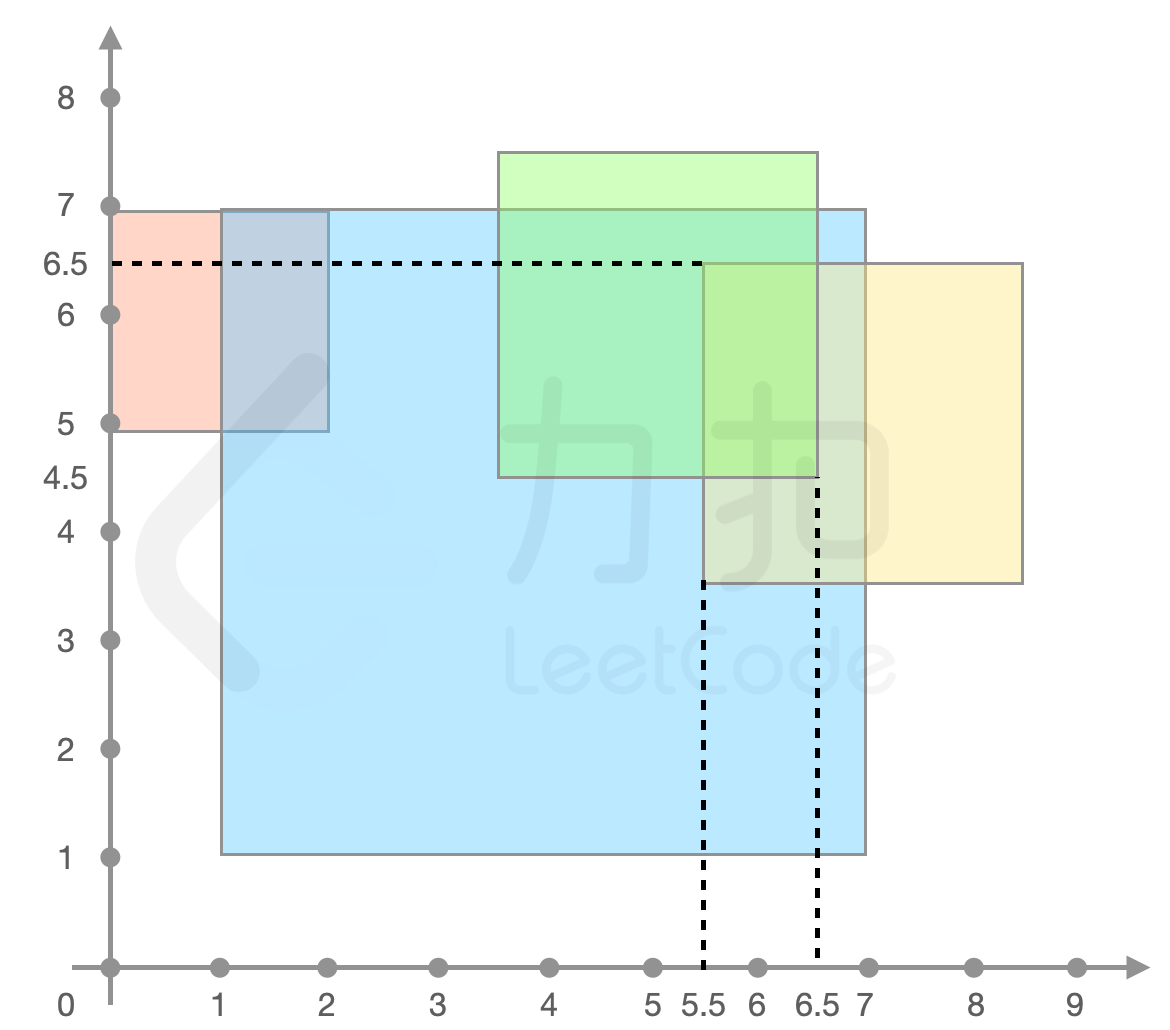{:width=500px}
|
||||
|
||||
|
||||
|
||||
**提示:**
|
||||
- `1 <= forceField.length <= 100`
|
||||
- `forceField[i].length == 3`
|
||||
- `0 <= forceField[i][0], forceField[i][1] <= 10^9`
|
||||
- `1 <= forceField[i][2] <= 10^9`
|
||||
@@ -0,0 +1,73 @@
|
||||
<p>请你编写一个函数,它接收一个异步函数 <code>fn</code> 和一个以毫秒为单位的时间 <code>t</code>。它应根据限时函数返回一个有 <strong>限时</strong> 效果的函数。</p>
|
||||
|
||||
<p>限时函数是与原函数相同的函数,除非它需要 <code>t</code> 毫秒以上的时间来完成。如果出现了这种情况,请你返回 <code>"Time Limit Exceeded"</code> 拒绝这次函数的调用。注意,它应该返回一个字符串拒绝,而不是一个 <code>Error</code> 。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><b>示例 1:</b></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
fn = async (n) => {
|
||||
await new Promise(res => setTimeout(res, 100));
|
||||
return n * n;
|
||||
}
|
||||
inputs = [5]
|
||||
t = 50
|
||||
<b>输出:</b>{"rejected":"Time Limit Exceeded","time":50}
|
||||
<b>解释:
|
||||
</b>提供的函数设置在 100ms 后执行完成,但是设置的超时时间为 50ms,所以在 t=50ms 时拒绝因为达到了超时时间。
|
||||
</pre>
|
||||
|
||||
<p><b>示例 2:</b></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
fn = async (n) => {
|
||||
await new Promise(res => setTimeout(res, 100));
|
||||
return n * n;
|
||||
}
|
||||
inputs = [5]
|
||||
t = 150
|
||||
<b>输出:</b>{"resolved":25,"time":100}
|
||||
<b>解释:</b>
|
||||
在 t=100ms 时执行 5*5=25 ,没有达到超时时间。
|
||||
</pre>
|
||||
|
||||
<p><b>示例 3:</b></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
fn = async (a, b) => {
|
||||
await new Promise(res => setTimeout(res, 120));
|
||||
return a + b;
|
||||
}
|
||||
inputs = [5,10]
|
||||
t = 150
|
||||
<b>输出:</b>{"resolved":15,"time":120}
|
||||
<b>解释:
|
||||
</b>在 t=120ms 时执行 5+10=15,没有达到超时时间。
|
||||
</pre>
|
||||
|
||||
<p><b>示例 4:</b></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
fn = async () => {
|
||||
throw "Error";
|
||||
}
|
||||
inputs = []
|
||||
t = 1000
|
||||
<b>输出:</b>{"rejected":"Error","time":0}
|
||||
<b>解释:</b>
|
||||
此函数始终丢出 Error</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><b>提示:</b></p>
|
||||
|
||||
<ul>
|
||||
<li><code>0 <= inputs.length <= 10</code></li>
|
||||
<li><code>0 <= t <= 1000</code></li>
|
||||
<li><code>fn 返回一个 Promise 对象</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,58 @@
|
||||
<p>编写一个类,它允许获取和设置键-值对,并且每个键都有一个 <strong>过期时间</strong> 。</p>
|
||||
|
||||
<p>该类有三个公共方法:</p>
|
||||
|
||||
<p><code>set(key, value, duration)</code> :接收参数为整型键 <code>key</code> 、整型值 <code>value</code> 和以毫秒为单位的持续时间 <code>duration</code> 。一旦 <code>duration</code> 到期后,这个键就无法访问。如果相同的未过期键已经存在,该方法将返回 <code>true</code> ,否则返回 <code>false</code> 。如果该键已经存在,则它的值和持续时间都应该被覆盖。</p>
|
||||
|
||||
<p><code>get(key)</code> :如果存在一个未过期的键,它应该返回这个键相关的值。否则返回 <code>-1</code> 。</p>
|
||||
|
||||
<p><code>count()</code> :返回未过期键的总数。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>
|
||||
["TimeLimitedCache", "set", "get", "count", "get"]
|
||||
[[], [1, 42, 100], [1], [], [1]]
|
||||
[0, 0, 50, 50, 150]
|
||||
<strong>输出:</strong> [null, false, 42, 1, -1]
|
||||
<strong>解释:</strong>
|
||||
在 t=0 时,缓存被构造。
|
||||
在 t=0 时,添加一个键值对 (1: 42) ,过期时间为 100ms 。因为该值不存在,因此返回false。
|
||||
在 t=50 时,请求 key=1 并返回值 42。
|
||||
在 t=50 时,调用 count() ,缓存中有一个未过期的键。
|
||||
在 t=100 时,key=1 到期。
|
||||
在 t=150 时,调用 get(1) ,返回 -1,因为缓存是空的。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>
|
||||
["TimeLimitedCache", "set", "set", "get", "get", "get", "count"]
|
||||
[[], [1, 42, 50], [1, 50, 100], [1], [1], [1], []]
|
||||
[0, 0, 40, 50, 120, 200, 250]
|
||||
<strong>输出:</strong> [null, false, true, 50, 50, -1]
|
||||
<strong>解释:</strong>
|
||||
在 t=0 时,缓存被构造。
|
||||
在 t=0 时,添加一个键值对 (1: 42) ,过期时间为 50ms。因为该值不存在,因此返回false。
|
||||
当 t=40 时,添加一个键值对 (1: 50) ,过期时间为 100ms。因为一个未过期的键已经存在,返回 true 并覆盖这个键的旧值。
|
||||
在 t=50 时,调用 get(1) ,返回 50。
|
||||
在 t=120 时,调用 get(1) ,返回 50。
|
||||
在 t=140 时,key=1 过期。
|
||||
在 t=200 时,调用 get(1) ,但缓存为空,因此返回 -1。
|
||||
在 t=250 时,count() 返回0 ,因为缓存是空的,没有未过期的键。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>0 <= key <= 10<sup>9</sup></code></li>
|
||||
<li><code>0 <= value <= 10<sup>9</sup></code></li>
|
||||
<li><code>0 <= duration <= 1000</code></li>
|
||||
<li><code>方法调用总数不会超过100</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,35 @@
|
||||
<p>给你一个字符串 <code>word</code> ,你可以向其中任何位置插入 "a"、"b" 或 "c" 任意次,返回使 <code>word</code> <strong>有效</strong> 需要插入的最少字母数。</p>
|
||||
|
||||
<p>如果字符串可以由 "abc" 串联多次得到,则认为该字符串 <strong>有效</strong> 。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre><strong>输入:</strong>word = "b"
|
||||
<strong>输出:</strong>2
|
||||
<strong>解释:</strong>在 "b" 之前插入 "a" ,在 "b" 之后插入 "c" 可以得到有效字符串 "<strong>a</strong>b<strong>c</strong>" 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre><strong>输入:</strong>word = "aaa"
|
||||
<strong>输出:</strong>6
|
||||
<strong>解释:</strong>在每个 "a" 之后依次插入 "b" 和 "c" 可以得到有效字符串 "a<strong>bc</strong>a<strong>bc</strong>a<strong>bc</strong>" 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 3:</strong></p>
|
||||
|
||||
<pre><strong>输入:</strong>word = "abc"
|
||||
<strong>输出:</strong>0
|
||||
<strong>解释:</strong>word 已经是有效字符串,不需要进行修改。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= word.length <= 50</code></li>
|
||||
<li><code>word</code> 仅由字母 "a"、"b" 和 "c" 组成。</li>
|
||||
</ul>
|
||||
@@ -0,0 +1,39 @@
|
||||
<p>给你一个下标从 <strong>0</strong> 开始的 <code>m x n</code> 整数矩阵 <code>grid</code> 。矩阵中某一列的宽度是这一列数字的最大 <strong>字符串长度</strong> 。</p>
|
||||
|
||||
<ul>
|
||||
<li>比方说,如果 <code>grid = [[-10], [3], [12]]</code> ,那么唯一一列的宽度是 <code>3</code> ,因为 <code>-10</code> 的字符串长度为 <code>3</code> 。</li>
|
||||
</ul>
|
||||
|
||||
<p>请你返回一个大小为 <code>n</code> 的整数数组 <code>ans</code> ,其中 <code>ans[i]</code> 是第 <code>i</code> 列的宽度。</p>
|
||||
|
||||
<p>一个有 <code>len</code> 个数位的整数 <code>x</code> ,如果是非负数,那么 <strong>字符串</strong><strong>长度</strong> 为 <code>len</code> ,否则为 <code>len + 1</code> 。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre><b>输入:</b>grid = [[1],[22],[333]]
|
||||
<b>输出:</b>[3]
|
||||
<b>解释:</b>第 0 列中,333 字符串长度为 3 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre><b>输入:</b>grid = [[-15,1,3],[15,7,12],[5,6,-2]]
|
||||
<b>输出:</b>[3,1,2]
|
||||
<b>解释:</b>
|
||||
第 0 列中,只有 -15 字符串长度为 3 。
|
||||
第 1 列中,所有整数的字符串长度都是 1 。
|
||||
第 2 列中,12 和 -2 的字符串长度都为 2 。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>m == grid.length</code></li>
|
||||
<li><code>n == grid[i].length</code></li>
|
||||
<li><code>1 <= m, n <= 100 </code></li>
|
||||
<li><code>-10<sup>9</sup> <= grid[r][c] <= 10<sup>9</sup></code></li>
|
||||
</ul>
|
||||
67
leetcode-cn/problem (Chinese)/柯里化 [curry].html
Normal file
67
leetcode-cn/problem (Chinese)/柯里化 [curry].html
Normal file
@@ -0,0 +1,67 @@
|
||||
<p>请你编写一个函数,它接收一个其他的函数,并返回该函数的 <strong>柯里化 </strong>后的形式。</p>
|
||||
|
||||
<p><strong>柯里化 </strong>函数的定义是接受与原函数相同数量或更少数量的参数,并返回另一个 <strong>柯里化</strong> 后的函数或与原函数相同的值。</p>
|
||||
|
||||
<p>实际上,当你调用原函数,如 <code>sum(1,2,3)</code> 时,它将调用 <strong>柯里化</strong> 函数的某个形式,如 <code>csum(1)(2)(3)</code>, <code>csum(1)(2,3)</code>, <code>csum(1,2)(3)</code>,或 <code>csum(1,2,3)</code> 。所有调用 <strong>柯里化</strong> 函数的方法都应该返回与原始函数相同的值。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
fn = function sum(a, b, c) { return a + b + c; }
|
||||
inputs = [[1],[2],[3]]
|
||||
<b>输出:</b>6
|
||||
<strong>解释:</strong>
|
||||
执行的代码是:
|
||||
const curriedSum = curry(fn);
|
||||
curriedSum(1)(2)(3) === 6;
|
||||
curriedSum(1)(2)(3) 应该返回像原函数 sum(1, 2, 3) 一样的值。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>
|
||||
fn = function sum(a, b, c) { return a + b + c; }
|
||||
inputs = [[1,2],[3]]]
|
||||
<b>输出:</b>6
|
||||
<strong>解释:</strong>
|
||||
curriedSum(1, 2)(3) 应该返回像原函数 sum(1, 2, 3) 一样的值。</pre>
|
||||
|
||||
<p><strong>示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>
|
||||
fn = function sum(a, b, c) { return a + b + c; }
|
||||
inputs = [[],[],[1,2,3]]
|
||||
<b>输出:</b>6
|
||||
<strong>解释:</strong>
|
||||
你应该能够以任何方式传递参数,包括一次性传递所有参数或完全不传递参数。
|
||||
curriedSum()()(1, 2, 3) 应该返回像原函数 sum(1, 2, 3) 一样的值。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 4:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>
|
||||
fn = function life() { return 42; }
|
||||
inputs = [[]]
|
||||
<b>输出:</b>42
|
||||
<strong>解释:</strong>
|
||||
柯里化一个没有接收参数,没做有效操作的函数。
|
||||
curriedLife() === 42
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= inputs.length <= 1000</code></li>
|
||||
<li><code>0 <= inputs[i][j] <= 10<sup>5</sup></code></li>
|
||||
<li><code>0 <= fn.length <= 1000</code></li>
|
||||
<li><code>inputs.flat().length == fn.length</code></li>
|
||||
<li><code>函数参数需要被显式定义</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,40 @@
|
||||
<p>请你编写一个函数,检查给定的对象是否是给定类或超类的实例。</p>
|
||||
|
||||
<p>可以传递给函数的数据类型没有限制。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>func = () => checkIfInstance(new Date(), Date)
|
||||
<b>输出:</b>true
|
||||
<strong>解释:</strong>根据定义,Date 构造函数返回的对象是 Date 的一个实例。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>func = () => { class Animal {}; class Dog extends Animal {}; return checkIfInstance(new Dog(), Animal); }
|
||||
<b>输出:</b>true
|
||||
<strong>解释:</strong>
|
||||
class Animal {};
|
||||
class Dog extends Animal {};
|
||||
checkIfInstance(new Dog(), Animal); // true
|
||||
|
||||
Dog 是 Animal 的子类。因此,Dog 对象同时是 Dog 和 Animal 的实例。</pre>
|
||||
|
||||
<p><strong>示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>func = () => checkIfInstance(Date, Date)
|
||||
<b>输出:</b>false
|
||||
<strong>解释:</strong>日期的构造函数在逻辑上不能是其自身的实例。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 4:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>func = () => checkIfInstance(5, Number)
|
||||
<b>输出:</b>true
|
||||
<strong>解释:</strong>5 是一个 Number。注意,"instanceof" 关键字将返回 false。</pre>
|
||||
@@ -0,0 +1,55 @@
|
||||
<p>给你一个长度为 <code>n</code> 的整数数组 <code>nums</code> ,请你求出每个长度为 <code>k</code> 的子数组的 <b>美丽值</b> 。</p>
|
||||
|
||||
<p>一个子数组的 <strong>美丽值</strong> 定义为:如果子数组中第 <code>x</code> <strong>小整数</strong> 是 <strong>负数</strong> ,那么美丽值为第 <code>x</code> 小的数,否则美丽值为 <code>0</code> 。</p>
|
||||
|
||||
<p>请你返回一个包含<em> </em><code>n - k + 1</code> 个整数的数组,<strong>依次</strong> 表示数组中从第一个下标开始,每个长度为 <code>k</code> 的子数组的<strong> 美丽值</strong> 。</p>
|
||||
|
||||
<ul>
|
||||
<li>
|
||||
<p>子数组指的是数组中一段连续 <strong>非空</strong> 的元素序列。</p>
|
||||
</li>
|
||||
</ul>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre><b>输入:</b>nums = [1,-1,-3,-2,3], k = 3, x = 2
|
||||
<b>输出:</b>[-1,-2,-2]
|
||||
<b>解释:</b>总共有 3 个 k = 3 的子数组。
|
||||
第一个子数组是 <code>[1, -1, -3]</code> ,第二小的数是负数 -1 。
|
||||
第二个子数组是 <code>[-1, -3, -2]</code> ,第二小的数是负数 -2 。
|
||||
第三个子数组是 <code>[-3, -2, 3] ,第二小的数是负数 -2 。</code></pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre><b>输入:</b>nums = [-1,-2,-3,-4,-5], k = 2, x = 2
|
||||
<b>输出:</b>[-1,-2,-3,-4]
|
||||
<b>解释:</b>总共有 4 个 k = 2 的子数组。
|
||||
<code>[-1, -2] 中第二小的数是负数 -1 。</code>
|
||||
<code>[-2, -3] 中第二小的数是负数 -2 。</code>
|
||||
<code>[-3, -4] 中第二小的数是负数 -3 。</code>
|
||||
<code>[-4, -5] 中第二小的数是负数 -4 。</code></pre>
|
||||
|
||||
<p><strong>示例 3:</strong></p>
|
||||
|
||||
<pre><b>输入:</b>nums = [-3,1,2,-3,0,-3], k = 2, x = 1
|
||||
<b>输出:</b>[-3,0,-3,-3,-3]
|
||||
<b>解释:</b>总共有 5 个 k = 2 的子数组。
|
||||
<code>[-3, 1] 中最小的数是负数 -3 。</code>
|
||||
<code>[1, 2] 中最小的数不是负数,所以美丽值为 0 。</code>
|
||||
<code>[2, -3] 中最小的数是负数 -3 。</code>
|
||||
<code>[-3, 0] 中最小的数是负数 -3 。</code>
|
||||
<code>[0, -3] 中最小的数是负数 -3 。</code></pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>n == nums.length </code></li>
|
||||
<li><code>1 <= n <= 10<sup>5</sup></code></li>
|
||||
<li><code>1 <= k <= n</code></li>
|
||||
<li><code>1 <= x <= k </code></li>
|
||||
<li><code>-50 <= nums[i] <= 50 </code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,37 @@
|
||||
<p>请你编写一个生成器函数,并返回一个可以生成 <strong>斐波那契数列</strong> 的生成器对象。</p>
|
||||
|
||||
<p><strong>斐波那契数列</strong> 的递推公式为 <code>X<sub>n</sub> = X<sub>n-1</sub> + X<sub>n-2</sub></code> 。</p>
|
||||
|
||||
<p>这个数列的前几个数字是 <code>0, 1, 1, 2, 3, 5, 8, 13</code> 。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>callCount = 5
|
||||
<b>输出:</b>[0,1,1,2,3]
|
||||
<strong>解释:</strong>
|
||||
const gen = fibGenerator();
|
||||
gen.next().value; // 0
|
||||
gen.next().value; // 1
|
||||
gen.next().value; // 1
|
||||
gen.next().value; // 2
|
||||
gen.next().value; // 3
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>callCount = 0
|
||||
<strong>输出:</strong>[]
|
||||
<b>解释:</b>gen.next() 永远不会被调用,所以什么也不会输出
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>0 <= callCount <= 50</code></li>
|
||||
</ul>
|
||||
32
leetcode-cn/problem (Chinese)/睡眠函数 [sleep].html
Normal file
32
leetcode-cn/problem (Chinese)/睡眠函数 [sleep].html
Normal file
@@ -0,0 +1,32 @@
|
||||
<p>请你编写一个异步函数,它接收一个正整数参数 <code>millis</code> ,并休眠这么多毫秒。要求此函数可以解析任何值。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><b>示例 1:</b></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>millis = 100
|
||||
<b>输出:</b>100
|
||||
<b>解释:</b>
|
||||
在 100ms 后此异步函数执行完时返回一个 Promise 对象
|
||||
let t = Date.now();
|
||||
sleep(100).then(() => {
|
||||
console.log(Date.now() - t); // 100
|
||||
});
|
||||
</pre>
|
||||
|
||||
<p><b>示例 2:</b></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>millis = 200
|
||||
<b>输出:</b>200
|
||||
<b>解释:</b>在 200ms 后函数执行完时返回一个 Promise 对象
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><b>提示:</b></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= millis <= 1000</code></li>
|
||||
</ul>
|
||||
58
leetcode-cn/problem (Chinese)/蜗牛排序 [snail-traversal].html
Normal file
58
leetcode-cn/problem (Chinese)/蜗牛排序 [snail-traversal].html
Normal file
@@ -0,0 +1,58 @@
|
||||
<p>请你编写一段代码为所有数组实现 <code>snail(rowsCount,colsCount)</code> 方法,该方法将 1D 数组转换为以蜗牛排序的模式的 2D 数组。无效的输入值应该输出一个空数组。当 <code>rowsCount * colsCount !==</code><code>nums.length</code> 时。这个输入被认为是无效的。</p>
|
||||
|
||||
<p>蜗牛排序从左上角的单元格开始,从当前数组的第一个值开始。然后,它从上到下遍历第一列,接着移动到右边的下一列,并从下到上遍历它。将这种模式持续下去,每列交替变换遍历方向,直到覆盖整个数组。例如,当给定输入数组 <code>[19, 10, 3, 7, 9, 8, 5, 2, 1, 17, 16, 14, 12, 18, 6, 13, 11, 20, 4, 15]</code> ,当 <code>rowsCount = 5</code> 且 <code>colsCount = 4</code> 时,需要输出矩阵如下图所示。注意,矩阵沿箭头方向对应于原数组中数字的顺序</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><img alt="Traversal Diagram" src="https://assets.leetcode.com/uploads/2023/04/10/screen-shot-2023-04-10-at-100006-pm.png" style="width: 275px; height: 343px;" /></p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><b>示例 1:</b></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
nums = [19, 10, 3, 7, 9, 8, 5, 2, 1, 17, 16, 14, 12, 18, 6, 13, 11, 20, 4, 15]
|
||||
rowsCount = 5
|
||||
colsCount = 4
|
||||
<b>输出:</b>
|
||||
[
|
||||
[19,17,16,15],
|
||||
[10,1,14,4],
|
||||
[3,2,12,20],
|
||||
[7,5,18,11],
|
||||
[9,8,6,13]
|
||||
]
|
||||
</pre>
|
||||
|
||||
<p><b>示例 2:</b></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
nums = [1,2,3,4]
|
||||
rowsCount = 1
|
||||
colsCount = 4
|
||||
<b>输出:</b>[[1, 2, 3, 4]]
|
||||
</pre>
|
||||
|
||||
<p><b>示例 3:</b></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
nums = [1,3]
|
||||
rowsCount = 2
|
||||
colsCount = 2
|
||||
<b>输出:</b>[]
|
||||
<strong>Explanation:</strong> 2 * 2 = 4, 且原数组 [1,3] 的长度为 2; 所以,输入是无效的。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><b>提示:</b></p>
|
||||
|
||||
<ul>
|
||||
<li><code>0 <= nums.length <= 250</code></li>
|
||||
<li><code>1 <= nums[i] <= 1000</code></li>
|
||||
<li><code>1 <= rowsCount <= 250</code></li>
|
||||
<li><code>1 <= colsCount <= 250</code></li>
|
||||
</ul>
|
||||
26
leetcode-cn/problem (Chinese)/补给马车 [hqCnmP].md
Normal file
26
leetcode-cn/problem (Chinese)/补给马车 [hqCnmP].md
Normal file
@@ -0,0 +1,26 @@
|
||||
远征队即将开启未知的冒险之旅,不过在此之前,将对补给车队进行最后的检查。`supplies[i]` 表示编号为 `i` 的补给马车装载的物资数量。
|
||||
考虑到车队过长容易被野兽偷袭,他们决定将车队的长度变为原来的一半(向下取整),计划为:
|
||||
- 找出车队中 **物资之和最小** 两辆 **相邻** 马车,将它们车辆的物资整合为一辆。若存在多组物资之和相同的马车,则取编号最小的两辆马车进行整合;
|
||||
- 重复上述操作直到车队长度符合要求。
|
||||
|
||||
请返回车队长度符合要求后,物资的分布情况。
|
||||
|
||||
**示例 1:**
|
||||
>输入:`supplies = [7,3,6,1,8]`
|
||||
>
|
||||
>输出:`[10,15]`
|
||||
>
|
||||
>解释:
|
||||
> 第 1 次合并,符合条件的两辆马车为 6,1,合并后的车队为 [7,3,7,8];
|
||||
> 第 2 次合并,符合条件的两辆马车为 (7,3) 和 (3,7),取编号最小的 (7,3),合并后的车队为 [10,7,8];
|
||||
> 第 3 次合并,符合条件的两辆马车为 7,8,合并后的车队为 [10,15];
|
||||
>返回 `[10,15]`
|
||||
|
||||
**示例 2:**
|
||||
>输入:`supplies = [1,3,1,5]`
|
||||
>
|
||||
>输出:`[5,5]`
|
||||
|
||||
**解释:**
|
||||
- `2 <= supplies.length <= 1000`
|
||||
- `1 <= supplies[i] <= 1000`
|
||||
35
leetcode-cn/problem (Chinese)/计数器 [counter].html
Normal file
35
leetcode-cn/problem (Chinese)/计数器 [counter].html
Normal file
@@ -0,0 +1,35 @@
|
||||
<p>请你编写并返回一个 <strong>计数器 </strong>函数,它接收一个整型参数 n 。这个 <strong>计数器 </strong>函数最初返回 n,每次调用它时返回前一个值加 1 的值 ( <code>n</code> , <code>n + 1</code> , <code>n + 2</code> ,等等)。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
n = 10
|
||||
["call","call","call"]
|
||||
<b>输出:</b>[10,11,12]
|
||||
<strong>解释:
|
||||
</strong>counter() = 10 // 第一次调用 counter(),返回 n。
|
||||
counter() = 11 // 返回上次调用的值加 1。
|
||||
counter() = 12 // 返回上次调用的值加 1。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
n = -2
|
||||
["call","call","call","call","call"]
|
||||
<b>输出:</b>[-2,-1,0,1,2]
|
||||
<b>解释:</b>counter() 最初返回 -2。然后在每个后续调用后增加 1。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>-1000<sup> </sup><= n <= 1000</code></li>
|
||||
<li><code>最多对 counter() 进行 1000 次调用</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,29 @@
|
||||
<p>给你一个正整数 <code>arrivalTime</code> 表示列车正点到站的时间(单位:小时),另给你一个正整数 <code>delayedTime</code> 表示列车延误的小时数。</p>
|
||||
|
||||
<p>返回列车实际到站的时间。</p>
|
||||
|
||||
<p>注意,该问题中的时间采用 24 小时制。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre><strong>输入:</strong>arrivalTime = 15, delayedTime = 5
|
||||
<strong>输出:</strong>20
|
||||
<strong>解释:</strong>列车正点到站时间是 15:00 ,延误 5 小时,所以列车实际到站的时间是 15 + 5 = 20(20:00)。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre><strong>输入:</strong>arrivalTime = 13, delayedTime = 11
|
||||
<strong>输出:</strong>0
|
||||
<strong>解释:</strong>列车正点到站时间是 13:00 ,延误 11 小时,所以列车实际到站的时间是 13 + 11 = 24(在 24 小时制中表示为 00:00 ,所以返回 0)。</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= arrivaltime < 24</code></li>
|
||||
<li><code>1 <= delayedTime <= 24</code></li>
|
||||
</ul>
|
||||
58
leetcode-cn/problem (Chinese)/记忆函数 II [memoize-ii].html
Normal file
58
leetcode-cn/problem (Chinese)/记忆函数 II [memoize-ii].html
Normal file
@@ -0,0 +1,58 @@
|
||||
<p>请你编写一个函数,它接收一个函数参数 <code>fn</code>,并返回该函数的 <strong>记忆化</strong> 后的结果。</p>
|
||||
|
||||
<p><strong>记忆函数</strong> 是一个对于相同的输入永远不会被调用两次的函数。相反,它将返回一个缓存值。</p>
|
||||
|
||||
<p><code>fn</code> 可以是任何函数,对于它接受什么类型的值没有限制。如果输入为 <code>===</code>,则认为输入相同。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>
|
||||
getInputs = () => [[2,2],[2,2],[1,2]]
|
||||
fn = function (a, b) { return a + b; }
|
||||
<b>输出:</b>[{"val":4,"calls":1},{"val":4,"calls":1},{"val":3,"calls":2}]
|
||||
<strong>解释:</strong>
|
||||
const inputs = getInputs();
|
||||
const memoized = memoize(fn);
|
||||
for (const arr of inputs) {
|
||||
memoized(...arr);
|
||||
}
|
||||
|
||||
对于参数为 (2, 2) 的输入: 2 + 2 = 4,需要调用 fn() 。
|
||||
对于参数为 (2, 2) 的输入: 2 + 2 = 4,这些输入此前调用过,因此不需要调用 fn() 。
|
||||
对于参数为 (1, 2) 的输入: 1 + 2 = 3,需要再次调用 fn(),总调用数为 2 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
getInputs = () => [[{},{}],[{},{}],[{},{}]]
|
||||
fn = function (a, b) { return a + b; }
|
||||
<b>输出:</b>[{"val":{},"calls":1},{"val":{},"calls":2},{"val":{},"calls":3}]
|
||||
<strong>解释:</strong>
|
||||
合并两个空对象总是会得到一个空对象。因为缓存命中,所以只有 1 次对 fn() 的调用,尽管这些对象之间没有一个是相同的(===)。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>
|
||||
getInputs = () => { const o = {}; return [[o,o],[o,o],[o,o]]; }
|
||||
fn = function (a, b) { return ({...a, ...b}); }
|
||||
<b>输出:</b>[{"val":{},"calls":1},{"val":{},"calls":1},{"val":{},"calls":1}]
|
||||
<strong>解释:</strong>
|
||||
合并两个空对象总是会得到一个空对象。第 2 和第 3 个函数调用导致缓存命中。这是因为传入的每个对象都是相同的。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= inputs.length <= 10<sup>5</sup></code></li>
|
||||
<li><code>0 <= inputs.flat().length <= 10<sup>5</sup></code></li>
|
||||
<li><code>inputs[i][j] != NaN</code></li>
|
||||
</ul>
|
||||
82
leetcode-cn/problem (Chinese)/记忆函数 [memoize].html
Normal file
82
leetcode-cn/problem (Chinese)/记忆函数 [memoize].html
Normal file
@@ -0,0 +1,82 @@
|
||||
<p>请你编写一个函数,它接收另一个函数作为输入,并返回该函数的 <strong>记忆化</strong> 后的结果。</p>
|
||||
|
||||
<p><strong>记忆函数</strong> 是一个对于相同的输入永远不会被调用两次的函数。相反,它将返回一个缓存值。</p>
|
||||
|
||||
<p>你可以假设有 <strong>3</strong> 个可能的输入函数:<code>sum</code> 、<code>fib</code> 和 <code>factorial</code> 。</p>
|
||||
|
||||
<ul>
|
||||
<li> <code>sum</code> 接收两个整型参数 <code>a</code> 和 <code>b</code> ,并返回 <code>a + b</code> 。</li>
|
||||
<li> <code>fib</code> 接收一个整型参数 <code>n</code> ,如果 <code>n <= 1</code> 则返回 <code>1</code>,否则返回 <code>fib (n - 1) + fib (n - 2)</code>。</li>
|
||||
<li> <code>factorial</code> 接收一个整型参数 <code>n</code> ,如果 <code>n <= 1</code> 则返回 <code>1</code> ,否则返回 <code>factorial(n - 1) * n</code> 。</li>
|
||||
</ul>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>
|
||||
"sum"
|
||||
["call","call","getCallCount","call","getCallCount"]
|
||||
[[2,2],[2,2],[],[1,2],[]]
|
||||
<strong>输出:</strong>
|
||||
[4,4,1,3,2]
|
||||
|
||||
<strong>解释:</strong>
|
||||
const sum = (a, b) => a + b;
|
||||
const memoizedSum = memoize(sum);
|
||||
memoizedSum (2, 2);// 返回 4。sum() 被调用,因为之前没有使用参数 (2, 2) 调用过。
|
||||
memoizedSum (2, 2);// 返回 4。没有调用 sum(),因为前面有相同的输入。
|
||||
//总调用数: 1
|
||||
memoizedSum(1、2);// 返回 3。sum() 被调用,因为之前没有使用参数 (1, 2) 调用过。
|
||||
//总调用数: 2
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:
|
||||
</strong>"factorial"
|
||||
["call","call","call","getCallCount","call","getCallCount"]
|
||||
[[2],[3],[2],[],[3],[]]
|
||||
<strong>输出:</strong>
|
||||
[2,6,2,2,6,2]
|
||||
|
||||
<strong>解释:</strong>
|
||||
const factorial = (n) => (n <= 1) ? 1 : (n * factorial(n - 1));
|
||||
const memoFactorial = memoize(factorial);
|
||||
memoFactorial(2); // 返回 2。
|
||||
memoFactorial(3); // 返回 6。
|
||||
memoFactorial(2); // 返回 2。 没有调用 factorial(),因为前面有相同的输入。
|
||||
// 总调用数:2
|
||||
memoFactorial(3); // 返回 6。 没有调用 factorial(),因为前面有相同的输入。
|
||||
// 总调用数:2
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:
|
||||
</strong>"fib"
|
||||
["call","getCallCount"]
|
||||
[[5],[]]
|
||||
<strong>输出:</strong>
|
||||
[8,1]
|
||||
|
||||
<strong>解释:
|
||||
</strong>fib(5) = 8
|
||||
// 总调用数:1
|
||||
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>Constraints:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>0 <= a, b <= 10<sup>5</sup></code></li>
|
||||
<li><code>1 <= n <= 10</code></li>
|
||||
<li><code>at most 10<sup>5</sup> function calls</code></li>
|
||||
<li><code>at most 10<sup>5</sup> attempts to access callCount</code></li>
|
||||
<li><code>input function is sum, fib, or factorial</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,44 @@
|
||||
<p>给你一个有 <code>n</code> 个节点的 <strong>有向带权</strong> 图,节点编号为 <code>0</code> 到 <code>n - 1</code> 。图中的初始边用数组 <code>edges</code> 表示,其中 <code>edges[i] = [from<sub>i</sub>, to<sub>i</sub>, edgeCost<sub>i</sub>]</code> 表示从 <code>from<sub>i</sub></code> 到 <code>to<sub>i</sub></code> 有一条代价为 <code>edgeCost<sub>i</sub></code> 的边。</p>
|
||||
|
||||
<p>请你实现一个 <code>Graph</code> 类:</p>
|
||||
|
||||
<ul>
|
||||
<li><code>Graph(int n, int[][] edges)</code> 初始化图有 <code>n</code> 个节点,并输入初始边。</li>
|
||||
<li><code>addEdge(int[] edge)</code> 向边集中添加一条边,其中<strong> </strong><code>edge = [from, to, edgeCost]</code> 。数据保证添加这条边之前对应的两个节点之间没有有向边。</li>
|
||||
<li><code>int shortestPath(int node1, int node2)</code> 返回从节点 <code>node1</code> 到 <code>node2</code> 的路径<strong> 最小</strong> 代价。如果路径不存在,返回 <code>-1</code> 。一条路径的代价是路径中所有边代价之和。</li>
|
||||
</ul>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<p><img alt="" src="https://assets.leetcode.com/uploads/2023/01/11/graph3drawio-2.png" style="width: 621px; height: 191px;"></p>
|
||||
|
||||
<pre><strong>输入:</strong>
|
||||
["Graph", "shortestPath", "shortestPath", "addEdge", "shortestPath"]
|
||||
[[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]]
|
||||
<b>输出:</b>
|
||||
[null, 6, -1, null, 6]
|
||||
|
||||
<strong>解释:</strong>
|
||||
Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]);
|
||||
g.shortestPath(3, 2); // 返回 6 。从 3 到 2 的最短路径如第一幅图所示:3 -> 0 -> 1 -> 2 ,总代价为 3 + 2 + 1 = 6 。
|
||||
g.shortestPath(0, 3); // 返回 -1 。没有从 0 到 3 的路径。
|
||||
g.addEdge([1, 3, 4]); // 添加一条节点 1 到节点 3 的边,得到第二幅图。
|
||||
g.shortestPath(0, 3); // 返回 6 。从 0 到 3 的最短路径为 0 -> 1 -> 3 ,总代价为 2 + 4 = 6 。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= n <= 100</code></li>
|
||||
<li><code>0 <= edges.length <= n * (n - 1)</code></li>
|
||||
<li><code>edges[i].length == edge.length == 3</code></li>
|
||||
<li><code>0 <= from<sub>i</sub>, to<sub>i</sub>, from, to, node1, node2 <= n - 1</code></li>
|
||||
<li><code>1 <= edgeCost<sub>i</sub>, edgeCost <= 10<sup>6</sup></code></li>
|
||||
<li>图中任何时候都不会有重边和自环。</li>
|
||||
<li>调用 <code>addEdge</code> 至多 <code>100</code> 次。</li>
|
||||
<li>调用 <code>shortestPath</code> 至多 <code>100</code> 次。</li>
|
||||
</ul>
|
||||
@@ -0,0 +1,137 @@
|
||||
<p>有时候你会有一个长时间运行的任务,并且你可能希望在它完成之前取消它。为了实现这个目标,请你编写一个名为 <code>cancellable</code> 的函数,它接收一个生成器对象,并返回一个包含两个值的数组:一个 <strong>取消函数</strong> 和一个 <strong>promise</strong> 对象。</p>
|
||||
|
||||
<p>你可以假设生成器函数只会生成 promise 对象。你的函数负责将 promise 对象解析的值传回生成器。如果 promise 被拒绝,你的函数应将该错误抛回给生成器。</p>
|
||||
|
||||
<p>如果在生成器完成之前调用了取消回调函数,则你的函数应该将错误抛回给生成器。该错误应该是字符串 <code>"Cancelled"</code>(而不是一个 <code>Error</code> 对象)。如果错误被捕获,则返回的 promise 应该解析为下一个生成或返回的值。否则,promise 应该被拒绝并抛出该错误。不应执行任何其他代码。</p>
|
||||
|
||||
<p>当生成器完成时,您的函数返回的 promise 应该解析为生成器返回的值。但是,如果生成器抛出错误,则返回的 promise 应该拒绝并抛出该错误。</p>
|
||||
|
||||
<p>下面是您的代码应如何使用的示例:</p>
|
||||
|
||||
<pre>
|
||||
function* tasks() {
|
||||
const val = yield new Promise(resolve => resolve(2 + 2));
|
||||
yield new Promise(resolve => setTimeout(resolve, 100));
|
||||
return val + 1; // calculation shouldn't be done.
|
||||
}
|
||||
const [cancel, promise] = cancellable(tasks());
|
||||
setTimeout(cancel, 50);
|
||||
promise.catch(console.log); // logs "Cancelled" at t=50ms
|
||||
</pre>
|
||||
|
||||
<p>如果相反, <code>cancel()</code> 没有被调用或者在 <code>t=100ms</code> 之后才被调用,那么 Promise 应被解析为 <code>5</code> 。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
generatorFunction = function*() {
|
||||
return 42;
|
||||
}
|
||||
cancelledAt = 100
|
||||
<b>输出:</b>{"resolved": 42}
|
||||
<strong>解释:</strong>
|
||||
const generator = generatorFunction();
|
||||
const [cancel, promise] = cancellable(generator);
|
||||
setTimeout(cancel, 100);
|
||||
promise.then(console.log); // 在 t=0ms 解析为 42
|
||||
|
||||
该生成器立即生成 42 并完成。因此,返回的 promise 立即解析为 42。请注意,取消已经完成的生成器没有任何作用。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>
|
||||
generatorFunction = function*() {
|
||||
const msg = yield new Promise(res => res("Hello"));
|
||||
throw `Error: ${msg}`;
|
||||
}
|
||||
cancelledAt = null
|
||||
<b>输出:</b>{"rejected": "Error: Hello"}
|
||||
<strong>解释:</strong>
|
||||
一个 Promise 被生成。该函数通过等待 promise 解析并将解析后的值传回生成器来处理它。然后抛出一个错误,这会导致 promise 被同样抛出的错误拒绝。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
generatorFunction = function*() {
|
||||
yield new Promise(res => setTimeout(res, 200));
|
||||
return "Success";
|
||||
}
|
||||
cancelledAt = 100
|
||||
<b>输出:</b>{"rejected": "Cancelled"}
|
||||
<strong>解释:</strong>
|
||||
当函数等待被生成的 promise 解析时,cancel() 被调用。这会导致一个错误消息被发送回生成器。由于这个错误没有被捕获,返回的 promise 会因为这个错误而被拒绝。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 4:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>
|
||||
generatorFunction = function*() {
|
||||
let result = 0;
|
||||
yield new Promise(res => setTimeout(res, 100));
|
||||
result += yield new Promise(res => res(1));
|
||||
yield new Promise(res => setTimeout(res, 100));
|
||||
result += yield new Promise(res => res(1));
|
||||
return result;
|
||||
}
|
||||
cancelledAt = null
|
||||
<b>输出:</b>{"resolved": 2}
|
||||
<strong>解释:</strong>
|
||||
生成器生成了 4 个 promise 。其中两个 promise 的值被添加到结果中。200ms 后,生成器以值 2 完成,该值被返回的 promise 解析。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 5:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
generatorFunction = function*() {
|
||||
let result = 0;
|
||||
try {
|
||||
yield new Promise(res => setTimeout(res, 100));
|
||||
result += yield new Promise(res => res(1));
|
||||
yield new Promise(res => setTimeout(res, 100));
|
||||
result += yield new Promise(res => res(1));
|
||||
} catch(e) {
|
||||
return result;
|
||||
}
|
||||
return result;
|
||||
}
|
||||
cancelledAt = 150
|
||||
<b>输出:</b>{"resolved": 1}
|
||||
<strong>解释:</strong>
|
||||
前两个生成的 promise 解析并导致结果递增。然而,在 t=150ms 时,生成器被取消了。发送给生成器的错误被捕获,结果被返回并最终由返回的 promise 解析。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 6:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
generatorFunction = function*() {
|
||||
try {
|
||||
yield new Promise((resolve, reject) => reject("Promise Rejected"));
|
||||
} catch(e) {
|
||||
let a = yield new Promise(resolve => resolve(2));
|
||||
let b = yield new Promise(resolve => resolve(2));
|
||||
return a + b;
|
||||
};
|
||||
}
|
||||
cancelledAt = null
|
||||
<b>输出:</b>{"resolved": 4}
|
||||
<strong>解释:</strong>
|
||||
第一个生成的 promise 立即被拒绝。该错误被捕获。因为生成器没有被取消,执行继续像往常一样。最终解析为 2 + 2 = 4。</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>cancelledAt == null or 0 <= cancelledAt <= 1000</code></li>
|
||||
<li><code>generatorFunction 返回一个生成器对象</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,44 @@
|
||||
<p>编写一个函数,这个函数接收一个整数数组 <code>arr</code> 和一个映射函数 <code>fn</code> ,通过该映射函数返回一个新的数组。</p>
|
||||
|
||||
<p>返回数组的创建语句应为 <code>returnedArray[i] = fn(arr[i], i)</code> 。</p>
|
||||
|
||||
<p>请你在不使用内置方法 <code>Array.map</code> 的前提下解决这个问题。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong class="example">示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>arr = [1,2,3], fn = function plusone(n) { return n + 1; }
|
||||
<strong>输出:</strong>[2,3,4]
|
||||
<strong>解释: </strong>
|
||||
const newArray = map(arr, plusone); // [2,3,4]
|
||||
此映射函数返回值是将数组中每个元素的值加 1。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例</strong><strong class="example"> 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>arr = [1,2,3], fn = function plusI(n, i) { return n + i; }
|
||||
<strong>输出:</strong>[1,3,5]
|
||||
<strong>解释:</strong>此映射函数返回值根据输入数组索引增加每个值。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>arr = [10,20,30], fn = function constant() { return 42; }
|
||||
<strong>输出:</strong>[42,42,42]
|
||||
<strong>解释:</strong>此映射函数返回值恒为 42。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>0 <= arr.length <= 1000</code></li>
|
||||
<li><code><font face="monospace">-10<sup>9</sup> <= arr[i] <= 10<sup>9</sup></font></code></li>
|
||||
<li><font face="monospace"><code>fn 返回一个数</code></font></li>
|
||||
</ul>
|
||||
<span style="display:block"><span style="height:0px"><span style="position:absolute"></span></span></span>
|
||||
@@ -0,0 +1,44 @@
|
||||
<p>请你编写一个函数,该函数接受一个整数数组参数 <code>arr</code> 和一个过滤函数 <code>fn</code>,并返回一个过滤后元素数量较少或元素数量相等的新数组。</p>
|
||||
|
||||
<p>返回的数组应该只包含通过过滤函数 <code>fn(arr[i], i)</code> 计算后为真值的元素。</p>
|
||||
|
||||
<p>请你在不使用内置函数 <code>Array.filter</code> 的前提下解决该问题。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong class="example">示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>arr = [0,10,20,30], fn = function greaterThan10(n) { return n > 10; }
|
||||
<b>输出:</b> [20,30]
|
||||
<b>解释:</b>
|
||||
const newArray = filter(arr, fn); // [20, 30]
|
||||
过滤函数过滤掉不大于 10 的值</pre>
|
||||
|
||||
<p><strong class="example">示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>arr = [1,2,3], fn = function firstIndex(n, i) { return i === 0; }
|
||||
<b>输出:</b>[1]
|
||||
<strong>解释:</strong>
|
||||
过滤函数 fn 也可以接受每个元素的索引
|
||||
在这种情况下,过滤函数删除索引不为 0 的元素
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>arr = [-2,-1,0,1,2], fn = function plusOne(n) { return n + 1 }
|
||||
<b>输出:</b>[-2,0,1,2]
|
||||
<strong>解释:</strong>
|
||||
像 0 这样的假值应被过滤掉
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>0 <= arr.length <= 1000</code></li>
|
||||
<li><code><font face="monospace">-10<sup>9</sup> <= arr[i] <= 10<sup>9</sup></font></code></li>
|
||||
</ul>
|
||||
32
leetcode-cn/problem (Chinese)/魔法棋盘 [1ybDKD].md
Normal file
32
leetcode-cn/problem (Chinese)/魔法棋盘 [1ybDKD].md
Normal file
@@ -0,0 +1,32 @@
|
||||
在大小为 `n * m` 的棋盘中,有两种不同的棋子:黑色,红色。当两颗颜色不同的棋子同时满足以下两种情况时,将会产生魔法共鸣:
|
||||
- 两颗异色棋子在同一行或者同一列
|
||||
- 两颗异色棋子之间恰好只有一颗棋子
|
||||
|
||||
由于棋盘上被施加了魔法禁制,棋盘上的部分格子变成问号。`chessboard[i][j]` 表示棋盘第 `i` 行 `j` 列的状态:
|
||||
- 若为 `.` ,表示当前格子确定为空
|
||||
- 若为 `B` ,表示当前格子确定为 黑棋
|
||||
- 若为 `R` ,表示当前格子确定为 红棋
|
||||
- 若为 `?` ,表示当前格子待定
|
||||
|
||||
现在,探险家小扣的任务是确定所有问号位置的状态(留空/放黑棋/放红棋),使最终的棋盘上,任意两颗棋子间都 **无法** 产生共鸣。请返回可以满足上述条件的放置方案数量。
|
||||
|
||||
**示例1:**
|
||||
> 输入:`n = 3, m = 3, chessboard = ["..R","..B","?R?"]`
|
||||
>
|
||||
> 输出:`5`
|
||||
>
|
||||
> 解释:给定的棋盘如图:
|
||||
>{:height=150px}
|
||||
> 所有符合题意的最终局面如图:
|
||||
>{:height=150px}
|
||||
|
||||
**示例2:**
|
||||
> 输入:`n = 3, m = 3, chessboard = ["?R?","B?B","?R?"]`
|
||||
>
|
||||
> 输出:`105`
|
||||
|
||||
**提示:**
|
||||
- `n == chessboard.length`
|
||||
- `m == chessboard[i].length`
|
||||
- `1 <= n*m <= 30`
|
||||
- `chessboard` 中仅包含 `"."、"B"、"R"、"?"`
|
||||
Reference in New Issue
Block a user