mirror of
https://gitee.com/coder-xiaomo/leetcode-problemset
synced 2025-12-11 21:30:58 +08:00
update
This commit is contained in:
58
leetcode-cn/problem (Chinese)/万灵之树 [cnHoX6].md
Normal file
58
leetcode-cn/problem (Chinese)/万灵之树 [cnHoX6].md
Normal file
@@ -0,0 +1,58 @@
|
||||
探险家小扣终于来到了万灵之树前,挑战最后的谜题。
|
||||
已知小扣拥有足够数量的链接节点和 `n` 颗幻境宝石,`gem[i]` 表示第 `i` 颗宝石的数值。现在小扣需要使用这些链接节点和宝石组合成一颗二叉树,其组装规则为:
|
||||
- 链接节点将作为二叉树中的非叶子节点,且每个链接节点必须拥有 `2` 个子节点;
|
||||
- 幻境宝石将作为二叉树中的叶子节点,所有的幻境宝石都必须被使用。
|
||||
|
||||
能量首先进入根节点,而后将按如下规则进行移动和记录:
|
||||
- 若能量首次到达该节点时:
|
||||
- 记录数字 `1`;
|
||||
- 若该节点为叶节点,将额外记录该叶节点的数值;
|
||||
- 若存在未到达的子节点,则选取未到达的一个子节点(优先选取左子节点)进入;
|
||||
- 若无子节点或所有子节点均到达过,此时记录 `9`,并回到当前节点的父节点(若存在)。
|
||||
|
||||
如果最终记下的数依序连接成一个整数 `num`,满足 $num \mod~p=target$,则视为解开谜题。
|
||||
请问有多少种二叉树的组装方案,可以使得最终记录下的数字可以解开谜题
|
||||
|
||||
**注意:**
|
||||
- 两棵结构不同的二叉树,作为不同的组装方案
|
||||
- 两棵结构相同的二叉树且存在某个相同位置处的宝石编号不同,也作为不同的组装方案
|
||||
- 可能存在数值相同的两颗宝石
|
||||
|
||||
**示例 1:**
|
||||
> 输入:`gem = [2,3]`
|
||||
> `p = 100000007`
|
||||
> `target = 11391299`
|
||||
>
|
||||
> 输出:`1`
|
||||
>
|
||||
> 解释:
|
||||
> 包含 `2` 个叶节点的结构只有一种。
|
||||
> 假设 B、C 节点的值分别为 3、2,对应 target 为 11391299,如下图所示。
|
||||
> 11391299 % 100000007 = 11391299,满足条件;
|
||||
> 假设 B、C 节点的值分别为 2、3,对应 target 为 11291399;
|
||||
> 11291399 % 100000007 = 11291399,不满足条件;
|
||||
> 因此只存在 1 种方案,返回 1
|
||||
.gif){:height=300px}
|
||||
|
||||
|
||||
**示例 2:**
|
||||
> 输入:`gem = [3,21,3]`
|
||||
> `p = 7`
|
||||
> `target = 5`
|
||||
>
|
||||
> 输出:`4`
|
||||
>
|
||||
> 解释:
|
||||
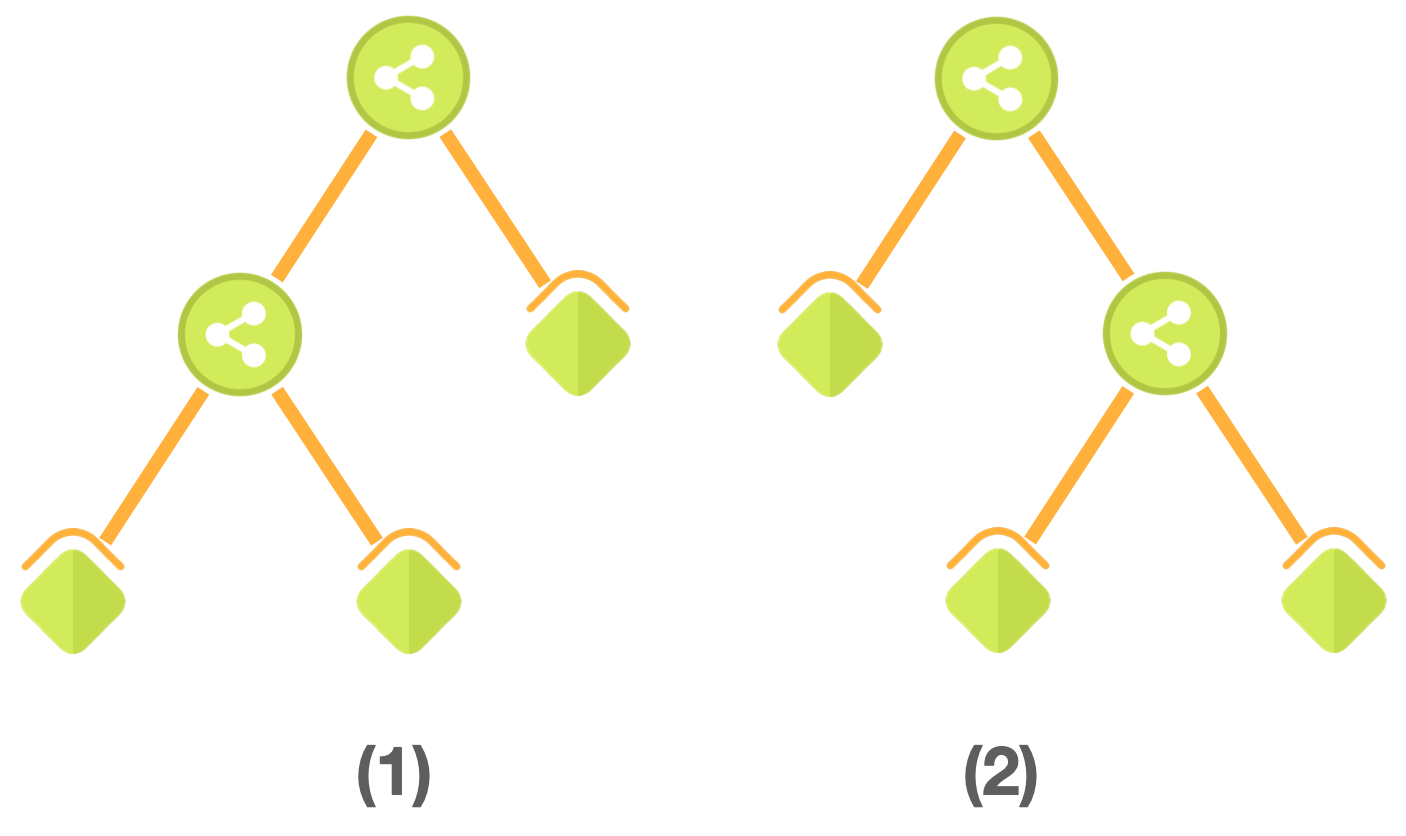
包含 `3` 个叶节点树结构有两种,列举如下:
|
||||
满足条件的组合有四种情况:
|
||||
> 当结构为下图(1)时:叶子节点的值为 [3,3,21] 或 [3,3,21],得到的整数为 `11139139912199`。
|
||||
> 当结构为下图(2)时:叶子节点的值为 [21,3,3] 或 [21,3,3],得到的整数为 `11219113913999`。
|
||||
{:width=500px}
|
||||
|
||||
|
||||
**提示:**
|
||||
- `1 <= gem.length <= 9`
|
||||
- `0 <= gem[i] <= 10^9`
|
||||
- `1 <= p <= 10^9`,保证 $p$ 为素数。
|
||||
- `0 <= target < p`
|
||||
- 存在 2 组 `gem.length == 9` 的用例
|
||||
54
leetcode-cn/problem (Chinese)/与非的谜题 [ryfUiz].md
Normal file
54
leetcode-cn/problem (Chinese)/与非的谜题 [ryfUiz].md
Normal file
@@ -0,0 +1,54 @@
|
||||
在永恒之森中,封存着有关万灵之树线索的卷轴,只要探险队通过最后的考验,便可以获取前往万灵之树的线索。
|
||||
|
||||
探险队需要从一段不断变化的谜题数组中找到最终的密码,初始的谜题为长度为 `n` 的数组 `arr`(下标从 0 开始),数组中的数字代表了 `k` 位二进制数。
|
||||
破解谜题的过程中,需要使用 `与非(NAND)` 运算方式,`operations[i] = [type,x,y]` 表示第 `i` 次进行的谜题操作信息:
|
||||
- 若 `type = 0`,表示修改操作,将谜题数组中下标 `x` 的数字变化为 `y`;
|
||||
- 若 `type = 1`,表示运算操作,将数字 `y` 进行 `x*n` 次「与非」操作,第 `i` 次与非操作为 `y = y NAND arr[i%n]`;
|
||||
> 运算操作结果即:`y NAND arr[0%n] NAND arr[1%n] NAND arr[2%n] ... NAND arr[(x*n-1)%n]`
|
||||
|
||||
最后,将所有运算操作的结果按顺序逐一进行 `异或(XOR)`运算,从而得到最终解开封印的密码。请返回最终解开封印的密码。
|
||||
|
||||
**注意:**
|
||||
- 「与非」(NAND)的操作为:先进行 `与` 操作,后进行 `非` 操作。
|
||||
> 例如:两个三位二进制数`2`和`3`,其与非结果为 `NOT ((010) AND (011)) = (101) = 5`
|
||||
|
||||
**示例 1:**
|
||||
> 输入:
|
||||
> `k = 3`
|
||||
> `arr = [1,2]`
|
||||
> `operations = [[1,2,3],[0,0,3],[1,2,2]]`
|
||||
>
|
||||
> 输出: `2`
|
||||
>
|
||||
> 解释:
|
||||
> 初始的谜题数组为 [1,2],二进制位数为 3,
|
||||
> 第 0 次进行运算操作,将数字 3(011) 进行 2\*2 次「与非」运算,
|
||||
> 运算操作结果为 `3 NAND 1 NAND 2 NAND 1 NAND 2 = 5`
|
||||
> 第 1 次进行修改操作,谜题数组的第 `0` 个数字变化为 `3`,谜题变成 `[3,2]`
|
||||
> 第 2 次进行运算操作,将数字 2(010) 进行 2\*2 次「与非」运算,
|
||||
> 运算操作结果为 `2 NAND 3 NAND 2 NAND 3 NAND 2 = 7`
|
||||
> 所有运算操作结果进行「异或」运算为 `5 XOR 7 = 2`
|
||||
> 因此得到的最终密码为 `2`。
|
||||
|
||||
**示例 2:**
|
||||
> 输入:
|
||||
> `k = 4`
|
||||
> `arr = [4,6,4,7,10,9,11]`
|
||||
> `operations = [[1,5,7],[1,7,14],[0,6,7],[1,6,5]]`
|
||||
> 输出: `9`
|
||||
> 解释:
|
||||
> 初始的谜题数组为 [4,6,4,7,10,9,11],
|
||||
> 第 0 次进行运算操作,运算操作结果为 5;
|
||||
> 第 1 次进行运算操作,运算操作结果为 5;
|
||||
> 第 2 次进行修改操作,修改后谜题数组为 [4, 6, 4, 7, 10, 9, 7];
|
||||
> 第 3 次进行运算操作,运算操作结果为 9;
|
||||
> 所有运算操作结果进行「异或」运算为 `5 XOR 5 XOR 9 = 9`;
|
||||
> 因此得到的最终密码为 `9`。
|
||||
|
||||
**提示:**
|
||||
- `1 <= arr.length, operations.length <= 10^4`
|
||||
- `1 <= k <= 30`
|
||||
- `0 <= arr[i] < 2^k`
|
||||
- 若 `type = 0`,`0 <= x < arr.length` 且 `0 <= y < 2^k`
|
||||
- 若 `type = 1`,`1 <= x < 10^9` 且 `0 <= y < 2^k`
|
||||
- 保证存在 `type = 1` 的操作
|
||||
@@ -0,0 +1,25 @@
|
||||
<p>二进制数转字符串。给定一个介于0和1之间的实数(如0.72),类型为double,打印它的二进制表达式。如果该数字无法精确地用32位以内的二进制表示,则打印“ERROR”。</p>
|
||||
|
||||
<p><strong>示例1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong> 输入</strong>:0.625
|
||||
<strong> 输出</strong>:"0.101"
|
||||
</pre>
|
||||
|
||||
<p><strong>示例2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong> 输入</strong>:0.1
|
||||
<strong> 输出</strong>:"ERROR"
|
||||
<strong> 提示</strong>:0.1无法被二进制准确表示
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li>32位包括输出中的 <code>"0."</code> 这两位。</li>
|
||||
<li>题目保证输入用例的小数位数最多只有 <code>6</code> 位</li>
|
||||
</ul>
|
||||
@@ -0,0 +1,51 @@
|
||||
<p>给你一个整数 <code>n</code> 表示一棵 <b>满二叉树</b> 里面节点的数目,节点编号从 <code>1</code> 到 <code>n</code> 。根节点编号为 <code>1</code> ,树中每个非叶子节点 <code>i</code> 都有两个孩子,分别是左孩子 <code>2 * i</code> 和右孩子 <code>2 * i + 1</code> 。</p>
|
||||
|
||||
<p>树中每个节点都有一个值,用下标从<b> 0</b> 开始、长度为 <code>n</code> 的整数数组 <code>cost</code> 表示,其中 <code>cost[i]</code> 是第 <code>i + 1</code> 个节点的值。每次操作,你可以将树中 <strong>任意</strong> 节点的值 <strong>增加</strong> <code>1</code> 。你可以执行操作 <strong>任意</strong> 次。</p>
|
||||
|
||||
<p>你的目标是让根到每一个 <strong>叶子结点</strong> 的路径值相等。请你返回 <strong>最少</strong> 需要执行增加操作多少次。</p>
|
||||
|
||||
<p><b>注意:</b></p>
|
||||
|
||||
<ul>
|
||||
<li><strong>满二叉树</strong> 指的是一棵树,它满足树中除了叶子节点外每个节点都恰好有 2 个节点,且所有叶子节点距离根节点距离相同。</li>
|
||||
<li><strong>路径值</strong> 指的是路径上所有节点的值之和。</li>
|
||||
</ul>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<p><img alt="" src="https://assets.leetcode.com/uploads/2023/04/04/binaryytreeedrawio-4.png" /></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>n = 7, cost = [1,5,2,2,3,3,1]
|
||||
<b>输出:</b>6
|
||||
<b>解释:</b>我们执行以下的增加操作:
|
||||
- 将节点 4 的值增加一次。
|
||||
- 将节点 3 的值增加三次。
|
||||
- 将节点 7 的值增加两次。
|
||||
从根到叶子的每一条路径值都为 9 。
|
||||
总共增加次数为 1 + 3 + 2 = 6 。
|
||||
这是最小的答案。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<p><img alt="" src="https://assets.leetcode.com/uploads/2023/04/04/binaryytreee2drawio.png" style="width: 205px; height: 151px;" /></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>n = 3, cost = [5,3,3]
|
||||
<b>输出:</b>0
|
||||
<b>解释:</b>两条路径已经有相等的路径值,所以不需要执行任何增加操作。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>3 <= n <= 10<sup>5</sup></code></li>
|
||||
<li><code>n + 1</code> 是 <code>2</code> 的幂</li>
|
||||
<li><code>cost.length == n</code></li>
|
||||
<li><code>1 <= cost[i] <= 10<sup>4</sup></code></li>
|
||||
</ul>
|
||||
48
leetcode-cn/problem (Chinese)/分块数组 [chunk-array].html
Normal file
48
leetcode-cn/problem (Chinese)/分块数组 [chunk-array].html
Normal file
@@ -0,0 +1,48 @@
|
||||
<p>给定一个数组 <code>arr</code> 和一个块大小 <code>size</code> ,返回一个 <strong>分块</strong> 的数组。<strong>分块</strong> 的数组包含了 <code>arr</code> 中的原始元素,但是每个子数组的长度都是 <code>size</code> 。如果 <code>arr.length</code> 不能被 <code>size</code> 整除,那么最后一个子数组的长度可能小于 <code>size</code> 。</p>
|
||||
|
||||
<p>你可以假设该数组是 <code>JSON.parse</code> 的输出结果。换句话说,它是有效的JSON。</p>
|
||||
|
||||
<p>请你在不使用 lodash 的函数 <code>_.chunk</code> 的情况下解决这个问题。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong class="example">示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>arr = [1,2,3,4,5], size = 1
|
||||
<b>输出:</b>[[1],[2],[3],[4],[5]]
|
||||
<b>解释:</b>数组 <code>arr </code>被分割成了每个只有一个元素的子数组。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>arr = [1,9,6,3,2], size = 3
|
||||
<b>输出:</b>[[1,9,6],[3,2]]
|
||||
<b>解释:</b>数组 <code>arr </code>被分割成了每个有三个元素的子数组。然而,第二个子数组只有两个元素。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>arr = [8,5,3,2,6], size = 6
|
||||
<b>输出:</b>[[8,5,3,2,6]]
|
||||
<b>解释:</b><code>size </code>大于 <code>arr.length </code>,因此所有元素都在第一个子数组中。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 4:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>arr = [], size = 1
|
||||
<b>输出:</b>[]
|
||||
<b>解释:</b>没有元素需要分块,因此返回一个空数组。</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><b>提示:</b></p>
|
||||
|
||||
<ul>
|
||||
<li><code>arr is a valid JSON array</code></li>
|
||||
<li><code>2 <= JSON.stringify(arr).length <= 10<sup>5</sup></code></li>
|
||||
<li><code>1 <= size <= arr.length + 1</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,34 @@
|
||||
请你编写一个名为 <code>createHelloWorld</code> 的函数。它应该返回一个新的函数,该函数总是返回 <code>"Hello World"</code> 。
|
||||
<p> </p>
|
||||
|
||||
<p><strong class="example">示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>args = []
|
||||
<b>输出:</b>"Hello World"
|
||||
<strong>解释:</strong>
|
||||
const f = createHelloWorld();
|
||||
f(); // "Hello World"
|
||||
|
||||
createHelloWorld 返回的函数应始终返回 "Hello World"。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>args = [{},null,42]
|
||||
<b>输出:</b>"Hello World"
|
||||
<strong>解释:</strong>
|
||||
const f = createHelloWorld();
|
||||
f({}, null, 42); // "Hello World"
|
||||
|
||||
可以传递任何参数给函数,但它应始终返回 "Hello World"。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>0 <= args.length <= 10</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,41 @@
|
||||
<p>给定一个函数 <code>fn</code> ,它返回一个新的函数,返回的函数与原始函数完全相同,只不过它确保 <code>fn</code> 最多被调用一次。</p>
|
||||
|
||||
<ul>
|
||||
<li>第一次调用返回的函数时,它应该返回与 <code>fn</code> 相同的结果。</li>
|
||||
<li>第一次后的每次调用,它应该返回 <code>undefined</code> 。</li>
|
||||
</ul>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><b>示例 1:</b></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>fn = (a,b,c) => (a + b + c), calls = [[1,2,3],[2,3,6]]
|
||||
<b>输出:</b>[{"calls":1,"value":6}]
|
||||
<strong>解释:</strong>
|
||||
const onceFn = once(fn);
|
||||
onceFn(1, 2, 3); // 6
|
||||
onceFn(2, 3, 6); // undefined, fn 没有被调用
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>fn = (a,b,c) => (a * b * c), calls = [[5,7,4],[2,3,6],[4,6,8]]
|
||||
<b>输出:</b>[{"calls":1,"value":140}]
|
||||
<strong>解释:</strong>
|
||||
const onceFn = once(fn);
|
||||
onceFn(5, 7, 4); // 140
|
||||
onceFn(2, 3, 6); // undefined, fn 没有被调用
|
||||
onceFn(4, 6, 8); // undefined, fn 没有被调用
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= calls.length <= 10</code></li>
|
||||
<li><code>1 <= calls[i].length <= 100</code></li>
|
||||
<li><code>2 <= JSON.stringify(calls).length <= 1000</code></li>
|
||||
</ul>
|
||||
32
leetcode-cn/problem (Chinese)/城墙防线 [Nsibyl].md
Normal file
32
leetcode-cn/problem (Chinese)/城墙防线 [Nsibyl].md
Normal file
@@ -0,0 +1,32 @@
|
||||
在探险营地间,小扣意外发现了一片城墙遗迹,在探索期间,却不巧遇到迁徙中的兽群向他迎面冲来。情急之下小扣吹响了他的苍蓝笛,随着笛声响起,遗迹中的城墙逐渐发生了横向膨胀。
|
||||
已知 `rampart[i] = [x,y]` 表示第 `i` 段城墙的初始所在区间。当城墙发生膨胀时,将遵循以下规则:
|
||||
- 所有的城墙会同时膨胀相等的长度;
|
||||
- 每个城墙可以向左、向右或向两个方向膨胀。
|
||||
|
||||
小扣为了确保自身的安全,需要在所有城墙均无重叠的情况下,让城墙尽可能的膨胀。请返回城墙可以膨胀的 **最大值** 。
|
||||
|
||||
**注意:**
|
||||
- 初始情况下,所有城墙均不重叠,且 `rampart` 中的元素升序排列;
|
||||
- 两侧的城墙可以向外无限膨胀。
|
||||
|
||||
**示例 1:**
|
||||
>输入:`rampart = [[0,3],[4,5],[7,9]]`
|
||||
>
|
||||
>输出:`3`
|
||||
>
|
||||
>解释:如下图所示:
|
||||
>`rampart[0]` 向左侧膨胀 3 个单位;
|
||||
>`rampart[2]` 向右侧膨胀 3 个单位;
|
||||
>`rampart[1]` 向左侧膨胀 1 个单位,向右膨胀 2 个单位。
|
||||
>不存在膨胀更多的方案,返回 3。
|
||||
{:width=750px}
|
||||
|
||||
**示例 2:**
|
||||
>输入:`rampart = [[1,2],[5,8],[11,15],[18,25]]`
|
||||
>
|
||||
>输出:`4`
|
||||
|
||||
**提示:**
|
||||
- `3 <= rampart.length <= 10^4`
|
||||
- `rampart[i].length == 2`
|
||||
- `0 <= rampart[i][0] < rampart[i][1] <= rampart[i+1][0] <= 10^8`
|
||||
@@ -0,0 +1,127 @@
|
||||
<p>编写一个函数,将对象数组 <code>arr</code> 转换为矩阵 <code>m</code> 。</p>
|
||||
|
||||
<p><code>arr</code> 是一个由对象组成的数组或一个数组。数组中的每个项都可以包含深层嵌套的子数组和子对象。它还可以包含数字、字符串、布尔值和空值。</p>
|
||||
|
||||
<p>矩阵 <code>m</code> 的第一行应该是列名。如果没有嵌套,列名是对象中的唯一键。如果存在嵌套,列名是对象中相应路径,以点号 <code>"."</code> 分隔。</p>
|
||||
|
||||
<p>剩余的每一行对应 <code>arr</code> 中的一个对象。矩阵中的每个值对应对象中的一个值。如果给定对象在给定列中没有值,则应该包含空字符串 <code>""</code> 。</p>
|
||||
|
||||
<p>矩阵中的列应按 <strong>字典升序</strong> 排列。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong class="example">示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
arr = [
|
||||
{"b": 1, "a": 2},
|
||||
{"b": 3, "a": 4}
|
||||
]
|
||||
<b>输出:</b>
|
||||
[
|
||||
["a", "b"],
|
||||
[2, 1],
|
||||
[4, 3]
|
||||
]
|
||||
|
||||
<strong>解释:</strong>
|
||||
两个对象中有两个唯一的列名:"a"和"b"。
|
||||
"a"对应[2, 4]。
|
||||
"b"对应[1, 3]。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
arr = [
|
||||
{"a": 1, "b": 2},
|
||||
{"c": 3, "d": 4},
|
||||
{}
|
||||
]
|
||||
<b>输出:</b>
|
||||
[
|
||||
["a", "b", "c", "d"],
|
||||
[1, 2, "", ""],
|
||||
["", "", 3, 4],
|
||||
["", "", "", ""]
|
||||
]
|
||||
|
||||
<strong>解释:</strong>
|
||||
有四个唯一的列名:"a"、"b"、"c"、"d"。
|
||||
第一个对象具有与"a"和"b"关联的值。
|
||||
第二个对象具有与"c"和"d"关联的值。
|
||||
第三个对象没有键,因此只是一行空字符串。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
arr = [
|
||||
{"a": {"b": 1, "c": 2}},
|
||||
{"a": {"b": 3, "d": 4}}
|
||||
]
|
||||
<b>输出:</b>
|
||||
[
|
||||
["a.b", "a.c", "a.d"],
|
||||
[1, 2, ""],
|
||||
[3, "", 4]
|
||||
]
|
||||
|
||||
<b>解释:</b>
|
||||
在这个例子中,对象是嵌套的。键表示每个值的完整路径,路径之间用句点分隔。
|
||||
有三个路径:"a.b"、"a.c"、"a.d"。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 4:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
arr = [
|
||||
[{"a": null}],
|
||||
[{"b": true}],
|
||||
[{"c": "x"}]
|
||||
]
|
||||
<strong>输出:</strong>
|
||||
[
|
||||
["0.a", "0.b", "0.c"],
|
||||
[null, "", ""],
|
||||
["", true, ""],
|
||||
["", "", "x"]
|
||||
]
|
||||
|
||||
<strong>解释:</strong>
|
||||
数组也被视为具有索引为键的对象。
|
||||
每个数组只有一个元素,所以键是"0.a"、"0.b"和"0.c"。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 5:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>
|
||||
arr = [
|
||||
{},
|
||||
{},
|
||||
{},
|
||||
]
|
||||
<b>输出:</b>
|
||||
[
|
||||
[],
|
||||
[],
|
||||
[],
|
||||
[]
|
||||
]
|
||||
|
||||
<strong>解释:</strong>
|
||||
没有键,所以每一行都是一个空数组。</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= arr.length <= 1000</code></li>
|
||||
<li><code>unique keys <= 1000</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,44 @@
|
||||
<p>给你一个下标从 <strong>0</strong> 开始的数组 <code>nums</code> ,数组长度为 <code>n</code> 。</p>
|
||||
|
||||
<p><code>nums</code> 的 <strong>不同元素数目差</strong> 数组可以用一个长度为 <code>n</code> 的数组 <code>diff</code> 表示,其中 <code>diff[i]</code> 等于前缀 <code>nums[0, ..., i]</code> 中不同元素的数目 <strong>减去</strong> 后缀 <code>nums[i + 1, ..., n - 1]</code> 中不同元素的数目。</p>
|
||||
|
||||
<p>返回<em> </em><code>nums</code> 的 <strong>不同元素数目差</strong> 数组。</p>
|
||||
|
||||
<p>注意 <code>nums[i, ..., j]</code> 表示 <code>nums</code> 的一个从下标 <code>i</code> 开始到下标 <code>j</code> 结束的子数组(包含下标 <code>i</code> 和 <code>j</code> 对应元素)。特别需要说明的是,如果 <code>i > j</code> ,则 <code>nums[i, ..., j]</code> 表示一个空子数组。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>nums = [1,2,3,4,5]
|
||||
<strong>输出:</strong>[-3,-1,1,3,5]
|
||||
<strong>解释:
|
||||
</strong>对于 i = 0,前缀中有 1 个不同的元素,而在后缀中有 4 个不同的元素。因此,diff[0] = 1 - 4 = -3 。
|
||||
对于 i = 1,前缀中有 2 个不同的元素,而在后缀中有 3 个不同的元素。因此,diff[1] = 2 - 3 = -1 。
|
||||
对于 i = 2,前缀中有 3 个不同的元素,而在后缀中有 2 个不同的元素。因此,diff[2] = 3 - 2 = 1 。
|
||||
对于 i = 3,前缀中有 4 个不同的元素,而在后缀中有 1 个不同的元素。因此,diff[3] = 4 - 1 = 3 。
|
||||
对于 i = 4,前缀中有 5 个不同的元素,而在后缀中有 0 个不同的元素。因此,diff[4] = 5 - 0 = 5 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>nums = [3,2,3,4,2]
|
||||
<strong>输出:</strong>[-2,-1,0,2,3]
|
||||
<strong>解释:</strong>
|
||||
对于 i = 0,前缀中有 1 个不同的元素,而在后缀中有 3 个不同的元素。因此,diff[0] = 1 - 3 = -2 。
|
||||
对于 i = 1,前缀中有 2 个不同的元素,而在后缀中有 3 个不同的元素。因此,diff[1] = 2 - 3 = -1 。
|
||||
对于 i = 2,前缀中有 2 个不同的元素,而在后缀中有 2 个不同的元素。因此,diff[2] = 2 - 2 = 0 。
|
||||
对于 i = 3,前缀中有 3 个不同的元素,而在后缀中有 1 个不同的元素。因此,diff[3] = 3 - 1 = 2 。
|
||||
对于 i = 4,前缀中有 3 个不同的元素,而在后缀中有 0 个不同的元素。因此,diff[4] = 3 - 0 = 3 。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= n == nums.length <= 50</code></li>
|
||||
<li><code>1 <= nums[i] <= 50</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,50 @@
|
||||
<p><code>n</code> 个朋友在玩游戏。这些朋友坐成一个圈,按 <strong>顺时针方向</strong> 从 <code>1</code> 到 <code>n</code> 编号。从第 <code>i</code> 个朋友的位置开始顺时针移动 <code>1</code> 步会到达第 <code>(i + 1)</code> 个朋友的位置(<code>1 <= i < n</code>),而从第 <code>n</code> 个朋友的位置开始顺时针移动 <code>1</code> 步会回到第 <code>1</code> 个朋友的位置。</p>
|
||||
|
||||
<p>游戏规则如下:</p>
|
||||
|
||||
<p>第 <code>1</code> 个朋友接球。</p>
|
||||
|
||||
<ul>
|
||||
<li>接着,第 <code>1</code> 个朋友将球传给距离他顺时针方向 <code>k</code> 步的朋友。</li>
|
||||
<li>然后,接球的朋友应该把球传给距离他顺时针方向 <code>2 * k</code> 步的朋友。</li>
|
||||
<li>接着,接球的朋友应该把球传给距离他顺时针方向 <code>3 * k</code> 步的朋友,以此类推。</li>
|
||||
</ul>
|
||||
|
||||
<p>换句话说,在第 <code>i</code> 轮中持有球的那位朋友需要将球传递给距离他顺时针方向 <code>i * k</code> 步的朋友。</p>
|
||||
|
||||
<p>当某个朋友第 2 次接到球时,游戏结束。</p>
|
||||
|
||||
<p>在整场游戏中没有接到过球的朋友是 <strong>输家</strong> 。</p>
|
||||
|
||||
<p>给你参与游戏的朋友数量 <code>n</code> 和一个整数 <code>k</code> ,请按升序排列返回包含所有输家编号的数组 <code>answer</code> 作为答案。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>n = 5, k = 2
|
||||
<strong>输出:</strong>[4,5]
|
||||
<strong>解释:</strong>以下为游戏进行情况:
|
||||
1)第 1 个朋友接球,第 <code>1</code> 个朋友将球传给距离他顺时针方向 2 步的玩家 —— 第 3 个朋友。
|
||||
2)第 3 个朋友将球传给距离他顺时针方向 4 步的玩家 —— 第 2 个朋友。
|
||||
3)第 2 个朋友将球传给距离他顺时针方向 6 步的玩家 —— 第 3 个朋友。
|
||||
4)第 3 个朋友接到两次球,游戏结束。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>n = 4, k = 4
|
||||
<strong>输出:</strong>[2,3,4]
|
||||
<strong>解释:</strong>以下为游戏进行情况:
|
||||
1)第 1 个朋友接球,第 <code>1</code> 个朋友将球传给距离他顺时针方向 4 步的玩家 —— 第 1 个朋友。
|
||||
2)第 1 个朋友接到两次球,游戏结束。</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= k <= n <= 50</code></li>
|
||||
</ul>
|
||||
29
leetcode-cn/problem (Chinese)/提取咒文 [kjpLFZ].md
Normal file
29
leetcode-cn/problem (Chinese)/提取咒文 [kjpLFZ].md
Normal file
@@ -0,0 +1,29 @@
|
||||
随着兽群逐渐远去,一座大升降机缓缓的从地下升到了远征队面前。借由这台升降机,他们将能够到达地底的永恒至森。
|
||||
在升降机的操作台上,是一个由魔法符号组成的矩阵,为了便于辨识,我们用小写字母来表示。 `matrix[i][j]` 表示矩阵第 `i` 行 `j` 列的字母。该矩阵上有一个提取装置,可以对所在位置的字母提取。
|
||||
提取装置初始位于矩阵的左上角 `[0,0]`,可以通过每次操作移动到上、下、左、右相邻的 1 格位置中。提取装置每次移动或每次提取均记为一次操作。
|
||||
|
||||
远征队需要按照顺序,从矩阵中逐一取出字母以组成 `mantra`,才能够成功的启动升降机。请返回他们 **最少** 需要消耗的操作次数。如果无法完成提取,返回 `-1`。
|
||||
|
||||
**注意:**
|
||||
- 提取装置可对同一位置的字母重复提取,每次提取一个
|
||||
- 提取字母时,需按词语顺序依次提取
|
||||
|
||||
**示例 1:**
|
||||
>输入:`matrix = ["sd","ep"], mantra = "speed"`
|
||||
>
|
||||
>输出:`10`
|
||||
>
|
||||
>解释:如下图所示
|
||||
.gif)
|
||||
|
||||
**示例 2:**
|
||||
>输入:`matrix = ["abc","daf","geg"], mantra = "sad"`
|
||||
>
|
||||
>输出:`-1`
|
||||
>
|
||||
>解释:矩阵中不存在 `s` ,无法提取词语
|
||||
|
||||
**提示:**
|
||||
- `0 < matrix.length, matrix[i].length <= 100`
|
||||
- `0 < mantra.length <= 100`
|
||||
- `matrix 和 mantra` 仅由小写字母组成
|
||||
33
leetcode-cn/problem (Chinese)/最大或值 [maximum-or].html
Normal file
33
leetcode-cn/problem (Chinese)/最大或值 [maximum-or].html
Normal file
@@ -0,0 +1,33 @@
|
||||
<p>给你一个下标从 <strong>0</strong> 开始长度为 <code>n</code> 的整数数组 <code>nums</code> 和一个整数 <code>k</code> 。每一次操作中,你可以选择一个数并将它乘 <code>2</code> 。</p>
|
||||
|
||||
<p>你最多可以进行 <code>k</code> 次操作,请你返回<em> </em><code>nums[0] | nums[1] | ... | nums[n - 1]</code> 的最大值。</p>
|
||||
|
||||
<p><code>a | b</code> 表示两个整数 <code>a</code> 和 <code>b</code> 的 <strong>按位或</strong> 运算。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>nums = [12,9], k = 1
|
||||
<b>输出:</b>30
|
||||
<b>解释:</b>如果我们对下标为 1 的元素进行操作,新的数组为 [12,18] 。此时得到最优答案为 12 和 18 的按位或运算的结果,也就是 30 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>nums = [8,1,2], k = 2
|
||||
<b>输出:</b>35
|
||||
<b>解释:</b>如果我们对下标 0 处的元素进行操作,得到新数组 [32,1,2] 。此时得到最优答案为 32|1|2 = 35 。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= nums.length <= 10<sup>5</sup></code></li>
|
||||
<li><code>1 <= nums[i] <= 10<sup>9</sup></code></li>
|
||||
<li><code>1 <= k <= 15</code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,45 @@
|
||||
<p>给你一个下标从 <strong>0</strong> 开始、长度为 <code>n</code> 的数组 <code>nums</code> 。一开始,所有元素都是 <strong>未染色</strong> (值为 <code>0</code> )的。</p>
|
||||
|
||||
<p>给你一个二维整数数组 <code>queries</code> ,其中 <code>queries[i] = [index<sub>i</sub>, color<sub>i</sub>]</code> 。</p>
|
||||
|
||||
<p>对于每个操作,你需要将数组 <code>nums</code> 中下标为 <code>index<sub>i</sub></code> 的格子染色为 <code>color<sub>i</sub></code> 。</p>
|
||||
|
||||
<p>请你返回一个长度与 <code>queries</code> 相等的数组<em> </em><code>answer</code><em> </em>,其中<em> </em><code>answer[i]</code>是前 <code>i</code> 个操作 <strong>之后</strong> ,相邻元素颜色相同的数目。</p>
|
||||
|
||||
<p>更正式的,<code>answer[i]</code> 是执行完前 <code>i</code> 个操作后,<code>0 <= j < n - 1</code> 的下标 <code>j</code> 中,满足 <code>nums[j] == nums[j + 1]</code> 且 <code>nums[j] != 0</code> 的数目。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>n = 4, queries = [[0,2],[1,2],[3,1],[1,1],[2,1]]
|
||||
<b>输出:</b>[0,1,1,0,2]
|
||||
<b>解释:</b>一开始数组 nums = [0,0,0,0] ,0 表示数组中还没染色的元素。
|
||||
- 第 1 个操作后,nums = [2,0,0,0] 。相邻元素颜色相同的数目为 0 。
|
||||
- 第 2 个操作后,nums = [2,2,0,0] 。相邻元素颜色相同的数目为 1 。
|
||||
- 第 3 个操作后,nums = [2,2,0,1] 。相邻元素颜色相同的数目为 1 。
|
||||
- 第 4 个操作后,nums = [2,1,0,1] 。相邻元素颜色相同的数目为 0 。
|
||||
- 第 5 个操作后,nums = [2,1,1,1] 。相邻元素颜色相同的数目为 2 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>n = 1, queries = [[0,100000]]
|
||||
<b>输出:</b>[0]
|
||||
<b>解释:</b>一开始数组 nums = [0] ,0 表示数组中还没染色的元素。
|
||||
- 第 1 个操作后,nums = [100000] 。相邻元素颜色相同的数目为 0 。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= n <= 10<sup>5</sup></code></li>
|
||||
<li><code>1 <= queries.length <= 10<sup>5</sup></code></li>
|
||||
<li><code>queries[i].length == 2</code></li>
|
||||
<li><code>0 <= index<sub>i</sub> <= n - 1</code></li>
|
||||
<li><code>1 <= color<sub>i</sub> <= 10<sup>5</sup></code></li>
|
||||
</ul>
|
||||
34
leetcode-cn/problem (Chinese)/生物进化录 [qoQAMX].md
Normal file
34
leetcode-cn/problem (Chinese)/生物进化录 [qoQAMX].md
Normal file
@@ -0,0 +1,34 @@
|
||||
在永恒之森中,存在着一本生物进化录,以 **一个树形结构** 记载了所有生物的演化过程。经过观察并整理了各节点间的关系,`parents[i]` 表示编号 `i` 节点的父节点编号(根节点的父节点为 `-1`)。
|
||||
|
||||
为了探索和记录其中的演化规律,队伍中的炼金术师提出了一种方法,可以以字符串的形式将其复刻下来,规则如下:
|
||||
- 初始只有一个根节点,表示演化的起点,依次记录 `01` 字符串中的字符,
|
||||
- 如果记录 `0`,则在当前节点下添加一个子节点,并将指针指向新添加的子节点;
|
||||
- 如果记录 `1`,则将指针回退到当前节点的父节点处。
|
||||
|
||||
现在需要应用上述的记录方法,复刻下它的演化过程。请返回能够复刻演化过程的字符串中, **字典序最小** 的 `01` 字符串。
|
||||
|
||||
**注意:**
|
||||
- 节点指针最终可以停在任何节点上,不一定要回到根节点。
|
||||
|
||||
**示例 1:**
|
||||
> 输入:`parents = [-1,0,0,2]`
|
||||
>
|
||||
> 输出:`"00110"`
|
||||
>
|
||||
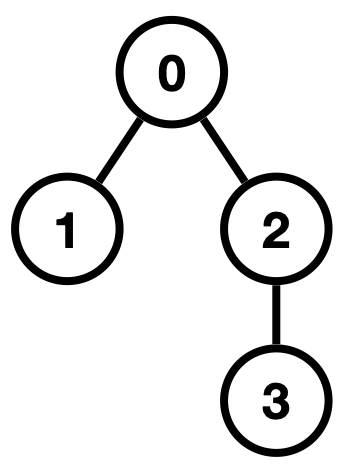
>解释:树结构如下图所示,共存在 2 种记录方案:
|
||||
>第 1 种方案为:0(记录编号 1 的节点) -> 1(回退至节点 0) -> 0(记录编号 2 的节点) -> 0((记录编号 3 的节点))
|
||||
>第 2 种方案为:0(记录编号 2 的节点) -> 0(记录编号 3 的节点) -> 1(回退至节点 2) -> 1(回退至节点 0) -> 0(记录编号 1 的节点)
|
||||
>返回字典序更小的 `"00110"`
|
||||
{:width=120px}.gif){:width=320px}
|
||||
|
||||
|
||||
|
||||
**示例 2:**
|
||||
> 输入:`parents = [-1,0,0,1,2,2]`
|
||||
>
|
||||
> 输出:`"00101100"`
|
||||
|
||||
**提示:**
|
||||
|
||||
- `1 <= parents.length <= 10^4`
|
||||
- `-1 <= parents[i] < i` (即父节点编号小于子节点)
|
||||
@@ -0,0 +1,54 @@
|
||||
<p>下标从 <strong>0</strong> 开始、长度为 <code>n</code> 的数组 <code>derived</code> 是由同样长度为 <code>n</code> 的原始 <strong>二进制数组</strong> <code>original</code> 通过计算相邻值的 <strong>按位异或(⊕)</strong>派生而来。</p>
|
||||
|
||||
<p>特别地,对于范围 <code>[0, n - 1]</code> 内的每个下标 <code>i</code> :</p>
|
||||
|
||||
<ul>
|
||||
<li>如果 <code>i = n - 1</code> ,那么 <code>derived[i] = original[i] ⊕ original[0]</code></li>
|
||||
<li>否则 <code>derived[i] = original[i] ⊕ original[i + 1]</code></li>
|
||||
</ul>
|
||||
|
||||
<p>给你一个数组 <code>derived</code> ,请判断是否存在一个能够派生得到 <code>derived</code> 的 <strong>有效原始二进制数组</strong> <code>original</code> 。</p>
|
||||
|
||||
<p>如果存在满足要求的原始二进制数组,返回 <em><strong>true</strong> </em>;否则,返回<em> <strong>false</strong> </em>。</p>
|
||||
|
||||
<ul>
|
||||
<li>二进制数组是仅由 <strong>0</strong> 和 <strong>1</strong> 组成的数组。</li>
|
||||
</ul>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre><strong>输入:</strong>derived = [1,1,0]
|
||||
<strong>输出:</strong>true
|
||||
<strong>解释:</strong>能够派生得到 [1,1,0] 的有效原始二进制数组是 [0,1,0] :
|
||||
derived[0] = original[0] ⊕ original[1] = 0 ⊕ 1 = 1
|
||||
derived[1] = original[1] ⊕ original[2] = 1 ⊕ 0 = 1
|
||||
derived[2] = original[2] ⊕ original[0] = 0 ⊕ 0 = 0
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre><strong>输入:</strong>derived = [1,1]
|
||||
<strong>输出:</strong>true
|
||||
<strong>解释:</strong>能够派生得到 [1,1] 的有效原始二进制数组是 [0,1] :
|
||||
derived[0] = original[0] ⊕ original[1] = 1
|
||||
derived[1] = original[1] ⊕ original[0] = 1
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 3:</strong></p>
|
||||
|
||||
<pre><strong>输入:</strong>derived = [1,0]
|
||||
<strong>输出:</strong>false
|
||||
<strong>解释:</strong>不存在能够派生得到 [1,0] 的有效原始二进制数组。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>n == derived.length</code></li>
|
||||
<li><code>1 <= n <= 10<sup>5</sup></code></li>
|
||||
<li><code>derived</code> 中的值不是 <strong>0</strong> 就是 <strong>1</strong> 。</li>
|
||||
</ul>
|
||||
35
leetcode-cn/problem (Chinese)/矩阵中的和 [sum-in-a-matrix].html
Normal file
35
leetcode-cn/problem (Chinese)/矩阵中的和 [sum-in-a-matrix].html
Normal file
@@ -0,0 +1,35 @@
|
||||
<p>给你一个下标从 <strong>0</strong> 开始的二维整数数组 <code>nums</code> 。一开始你的分数为 <code>0</code> 。你需要执行以下操作直到矩阵变为空:</p>
|
||||
|
||||
<ol>
|
||||
<li>矩阵中每一行选取最大的一个数,并删除它。如果一行中有多个最大的数,选择任意一个并删除。</li>
|
||||
<li>在步骤 1 删除的所有数字中找到最大的一个数字,将它添加到你的 <strong>分数</strong> 中。</li>
|
||||
</ol>
|
||||
|
||||
<p>请你返回最后的 <strong>分数</strong> 。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>nums = [[7,2,1],[6,4,2],[6,5,3],[3,2,1]]
|
||||
<b>输出:</b>15
|
||||
<b>解释:</b>第一步操作中,我们删除 7 ,6 ,6 和 3 ,将分数增加 7 。下一步操作中,删除 2 ,4 ,5 和 2 ,将分数增加 5 。最后删除 1 ,2 ,3 和 1 ,将分数增加 3 。所以总得分为 7 + 5 + 3 = 15 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>nums = [[1]]
|
||||
<b>输出:</b>1
|
||||
<b>解释:</b>我们删除 1 并将分数增加 1 ,所以返回 1 。</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= nums.length <= 300</code></li>
|
||||
<li><code>1 <= nums[i].length <= 500</code></li>
|
||||
<li><code>0 <= nums[i][j] <= 10<sup>3</sup></code></li>
|
||||
</ul>
|
||||
@@ -0,0 +1,41 @@
|
||||
<p>给你一个下标从 <strong>0</strong> 开始、大小为 <code>m x n</code> 的矩阵 <code>grid</code> ,矩阵由若干 <strong>正</strong> 整数组成。</p>
|
||||
|
||||
<p>你可以从矩阵第一列中的 <strong>任一</strong> 单元格出发,按以下方式遍历 <code>grid</code> :</p>
|
||||
|
||||
<ul>
|
||||
<li>从单元格 <code>(row, col)</code> 可以移动到 <code>(row - 1, col + 1)</code>、<code>(row, col + 1)</code> 和 <code>(row + 1, col + 1)</code> 三个单元格中任一满足值 <strong>严格</strong> 大于当前单元格的单元格。</li>
|
||||
</ul>
|
||||
|
||||
<p>返回你在矩阵中能够 <strong>移动</strong> 的 <strong>最大</strong> 次数。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
<img alt="" src="https://assets.leetcode.com/uploads/2023/04/11/yetgriddrawio-10.png" style="width: 201px; height: 201px;">
|
||||
<pre><strong>输入:</strong>grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
|
||||
<strong>输出:</strong>3
|
||||
<strong>解释:</strong>可以从单元格 (0, 0) 开始并且按下面的路径移动:
|
||||
- (0, 0) -> (0, 1).
|
||||
- (0, 1) -> (1, 2).
|
||||
- (1, 2) -> (2, 3).
|
||||
可以证明这是能够移动的最大次数。</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre><img alt="" src="https://assets.leetcode.com/uploads/2023/04/12/yetgrid4drawio.png">
|
||||
<strong>输入:</strong>grid = [[3,2,4],[2,1,9],[1,1,7]]
|
||||
<strong>输出:</strong>0
|
||||
<strong>解释:</strong>从第一列的任一单元格开始都无法移动。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>m == grid.length</code></li>
|
||||
<li><code>n == grid[i].length</code></li>
|
||||
<li><code>2 <= m, n <= 1000</code></li>
|
||||
<li><code>4 <= m * n <= 10<sup>5</sup></code></li>
|
||||
<li><code>1 <= grid[i][j] <= 10<sup>6</sup></code></li>
|
||||
</ul>
|
||||
26
leetcode-cn/problem (Chinese)/符文储备 [W2ZX4X].md
Normal file
26
leetcode-cn/problem (Chinese)/符文储备 [W2ZX4X].md
Normal file
@@ -0,0 +1,26 @@
|
||||
远征队在出发前需要携带一些「符文」,作为后续的冒险储备。`runes[i]` 表示第 `i` 枚符文的魔力值。
|
||||
|
||||
他们将从中选取若干符文进行携带,并对这些符文进行重新排列,以确保任意相邻的两块符文之间的魔力值相差不超过 `1`。
|
||||
|
||||
请返回他们能够携带的符文 **最大数量**。
|
||||
|
||||
**示例 1:**
|
||||
>输入:`runes = [1,3,5,4,1,7]`
|
||||
>
|
||||
>输出:`3`
|
||||
>
|
||||
>解释:最佳的选择方案为[3,5,4]
|
||||
>将其排列为 [3,4,5] 后,任意相邻的两块符文魔力值均不超过 `1`,携带数量为 `3`
|
||||
>其他满足条件的方案为 [1,1] 和 [7],数量均小于 3。
|
||||
>因此返回可携带的最大数量 `3`。
|
||||
|
||||
**示例 2:**
|
||||
>输入:`runes = [1,1,3,3,2,4]`
|
||||
>
|
||||
>输出:`6`
|
||||
>
|
||||
>解释:排列为 [1,1,2,3,3,4],可携带所有的符文
|
||||
|
||||
**提示:**
|
||||
- `1 <= runes.length <= 10^4`
|
||||
- `0 <= runes[i] <= 10^4`
|
||||
@@ -0,0 +1,44 @@
|
||||
<p>给你一个整数 <code>n</code> 。现有一个包含 <code>n</code> 个顶点的 <strong>无向</strong> 图,顶点按从 <code>0</code> 到 <code>n - 1</code> 编号。给你一个二维整数数组 <code>edges</code> 其中 <code>edges[i] = [a<sub>i</sub>, b<sub>i</sub>]</code> 表示顶点 <code>a<sub>i</sub></code> 和 <code>b<sub>i</sub></code> 之间存在一条 <strong>无向</strong> 边。</p>
|
||||
|
||||
<p>返回图中 <strong>完全连通分量</strong> 的数量。</p>
|
||||
|
||||
<p>如果在子图中任意两个顶点之间都存在路径,并且子图中没有任何一个顶点与子图外部的顶点共享边,则称其为 <strong>连通分量</strong> 。</p>
|
||||
|
||||
<p>如果连通分量中每对节点之间都存在一条边,则称其为 <strong>完全连通分量</strong> 。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<p><strong><img alt="" src="https://assets.leetcode.com/uploads/2023/04/11/screenshot-from-2023-04-11-23-31-23.png" style="width: 671px; height: 270px;" /></strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>n = 6, edges = [[0,1],[0,2],[1,2],[3,4]]
|
||||
<strong>输出:</strong>3
|
||||
<strong>解释:</strong>如上图所示,可以看到此图所有分量都是完全连通分量。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<p><strong><img alt="" src="https://assets.leetcode.com/uploads/2023/04/11/screenshot-from-2023-04-11-23-32-00.png" style="width: 671px; height: 270px;" /></strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入:</strong>n = 6, edges = [[0,1],[0,2],[1,2],[3,4],[3,5]]
|
||||
<strong>输出:</strong>1
|
||||
<strong>解释:</strong>包含节点 0、1 和 2 的分量是完全连通分量,因为每对节点之间都存在一条边。
|
||||
包含节点 3 、4 和 5 的分量不是完全连通分量,因为节点 4 和 5 之间不存在边。
|
||||
因此,在图中完全连接分量的数量是 1 。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= n <= 50</code></li>
|
||||
<li><code>0 <= edges.length <= n * (n - 1) / 2</code></li>
|
||||
<li><code>edges[i].length == 2</code></li>
|
||||
<li><code>0 <= a<sub>i</sub>, b<sub>i</sub> <= n - 1</code></li>
|
||||
<li><code>a<sub>i</sub> != b<sub>i</sub></code></li>
|
||||
<li>不存在重复的边</li>
|
||||
</ul>
|
||||
@@ -0,0 +1,40 @@
|
||||
<p>给你一个下标从 <strong>0</strong> 开始的字符串 <code>details</code> 。<code>details</code> 中每个元素都是一位乘客的信息,信息用长度为 <code>15</code> 的字符串表示,表示方式如下:</p>
|
||||
|
||||
<ul>
|
||||
<li>前十个字符是乘客的手机号码。</li>
|
||||
<li>接下来的一个字符是乘客的性别。</li>
|
||||
<li>接下来两个字符是乘客的年龄。</li>
|
||||
<li>最后两个字符是乘客的座位号。</li>
|
||||
</ul>
|
||||
|
||||
<p>请你返回乘客中年龄 <strong>严格大于 60 岁</strong> 的人数。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>details = ["7868190130M7522","5303914400F9211","9273338290F4010"]
|
||||
<b>输出:</b>2
|
||||
<b>解释:</b>下标为 0 ,1 和 2 的乘客年龄分别为 75 ,92 和 40 。所以有 2 人年龄大于 60 岁。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>details = ["1313579440F2036","2921522980M5644"]
|
||||
<b>输出:</b>0
|
||||
<b>解释:</b>没有乘客的年龄大于 60 岁。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= details.length <= 100</code></li>
|
||||
<li><code>details[i].length == 15</code></li>
|
||||
<li><code>details[i]</code> 中的数字只包含 <code>'0'</code> 到 <code>'9'</code> 。</li>
|
||||
<li><code>details[i][10]</code> 是 <code>'M'</code> ,<code>'F'</code> 或者 <code>'O'</code> 之一。</li>
|
||||
<li>所有乘客的手机号码和座位号互不相同。</li>
|
||||
</ul>
|
||||
50
leetcode-cn/problem (Chinese)/节流 [throttle].html
Normal file
50
leetcode-cn/problem (Chinese)/节流 [throttle].html
Normal file
@@ -0,0 +1,50 @@
|
||||
<p>现给定一个函数 <code>fn</code> 和一个以毫秒为单位的时间 <code>t</code> ,请你返回该函数的 <strong>节流</strong> 版本。</p>
|
||||
|
||||
<p><strong>节流</strong> 函数首先立即被调用,然后在 <code>t</code> 毫秒的时间间隔内不能再次执行,但应该存储最新的函数参数,以便在延迟结束后使用这些参数调用 <code>fn</code> 。</p>
|
||||
|
||||
<p>例如,<code>t = 50ms</code> ,并且函数在 <code>30ms</code> 、 <code>40ms</code> 和 <code>60ms</code> 时被调用。第一次函数调用会在接下来的 <code>t</code> 毫秒内阻止调用函数。第二次函数调用会保存参数,而第三次调用的参数应该覆盖当前保存的第二次调用的参数,因为第二次和第三次调用发生在 <code>80ms</code> 之前。一旦延迟时间过去,节流函数应该使用延迟期间提供的最新参数进行调用,并且还应创建另一个延迟期间,时长为 <code>80ms + t</code> 。</p>
|
||||
|
||||
<p><img alt="Throttle Diagram" src="https://assets.leetcode.com/uploads/2023/04/08/screen-shot-2023-04-08-at-120313-pm.png" style="width: 1156px; height: 372px;" />上面的图示展示了节流如何转换事件。每个矩形代表100毫秒,节流时间为400毫秒。每种颜色代表不同的输入集合。</p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong class="example">示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>t = 100, calls = [{"t":20,"inputs":[1]}]
|
||||
<b>输出:</b>[{"t":20,"inputs":[1]}]
|
||||
<b>解释:</b>第一次调用总是立即执行,没有延迟。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>t = 50, calls = [{"t":50,"inputs":[1]},{"t":75,"inputs":[2]}]
|
||||
<b>输出:</b>[{"t":50,"inputs":[1]},{"t":100,"inputs":[2]}]
|
||||
<b>解释:</b>
|
||||
第一次调用立即执行带有参数 (1) 的函数。
|
||||
第二次调用发生在 75毫秒 时,在延迟期间内,因为 50毫秒 + 50毫秒 = 100毫秒,所以下一次调用可以在 100毫秒 时执行。因此,我们保存第二次调用的参数,以便在第一次调用的回调函数中使用。
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>t = 70, calls = [{"t":50,"inputs":[1]},{"t":75,"inputs":[2]},{"t":90,"inputs":[8]},{"t": 140, "inputs":[5,7]},{"t": 300, "inputs": [9,4]}]
|
||||
<b>输出:</b>[{"t":50,"inputs":[1]},{"t":120,"inputs":[8]},{"t":190,"inputs":[5,7]},{"t":300,"inputs":[9,4]}]
|
||||
<b>解释:</b>
|
||||
第一次调用立即执行带有参数 (1) 的函数。
|
||||
第二次调用发生在 75毫秒 时,在延迟期间内,因为 50毫秒 + 70毫秒 = 120毫秒,所以它只应保存参数。
|
||||
第三次调用也在延迟期间内,因为我们只需要最新的函数参数,所以覆盖之前的参数。延迟期过后,在 120毫秒时进行回调,并使用保存的参数进行调用。该回调会创建另一个延迟期间,时长为 120毫秒 + 70毫秒 = 190毫秒,以便下一个函数可以在 190毫秒时调用。
|
||||
第四次调用发生在 140毫秒,在延迟期间内,因此应在190毫秒时作为回调进行调用。这将创建另一个延迟期间,时长为 190毫秒 + 70毫秒 = 260毫秒。
|
||||
第五次调用发生在 300毫秒,但它是在 260毫秒 之后,所以应立即调用,并创建另一个延迟期间,时长为 300毫秒 + 70毫秒 = 370毫秒。</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>0 <= t <= 1000</code></li>
|
||||
<li><code>1 <= calls.length <= 10</code></li>
|
||||
<li><code>0 <= calls[i].t <= 1000</code></li>
|
||||
<li><code>0 <= calls[i].inputs[i], calls[i].inputs.length <= 10</code></li>
|
||||
</ul>
|
||||
42
leetcode-cn/problem (Chinese)/英雄的力量 [power-of-heroes].html
Normal file
42
leetcode-cn/problem (Chinese)/英雄的力量 [power-of-heroes].html
Normal file
@@ -0,0 +1,42 @@
|
||||
<p>给你一个下标从 <strong>0</strong> 开始的整数数组 <code>nums</code> ,它表示英雄的能力值。如果我们选出一部分英雄,这组英雄的 <strong>力量</strong> 定义为:</p>
|
||||
|
||||
<ul>
|
||||
<li><code>i<sub>0</sub></code> ,<code>i<sub>1</sub></code> ,<span style="">... </span><code><span style="">i<sub>k</sub></span></code><span style=""> </span>表示这组英雄在数组中的下标。那么这组英雄的力量为 <code><font face="monospace">max(nums[</font>i<sub>0</sub><font face="monospace">],nums[</font>i<sub>1</sub><font face="monospace">] ... nums[</font><span style="font-size:10.8333px">i<sub>k</sub></span><font face="monospace">])<sup>2</sup> * min(nums[</font>i<sub>0</sub><font face="monospace">],nums[</font>i<sub>1</sub><font face="monospace">] ... nums[</font><span style="font-size:10.8333px">i<sub>k</sub></span><font face="monospace">])</font></code> 。</li>
|
||||
</ul>
|
||||
|
||||
<p>请你返回所有可能的 <strong>非空</strong> 英雄组的 <strong>力量</strong> 之和。由于答案可能非常大,请你将结果对 <code>10<sup>9 </sup>+ 7</code> <strong>取余。</strong></p>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>nums = [2,1,4]
|
||||
<b>输出:</b>141
|
||||
<b>解释:</b>
|
||||
第 1 组:[2] 的力量为 2<sup>2</sup> * 2 = 8 。
|
||||
第 2 组:[1] 的力量为 1<sup>2</sup> * 1 = 1 。
|
||||
第 3 组:[4] 的力量为 4<sup>2</sup> * 4 = 64 。
|
||||
第 4 组:[2,1] 的力量为 2<sup>2</sup> * 1 = 4 。
|
||||
第 5 组:[2,4] 的力量为 4<sup>2</sup> * 2 = 32 。
|
||||
第 6 组:[1,4] 的力量为 4<sup>2</sup> * 1 = 16 。
|
||||
第 7 组:[2,1,4] 的力量为 4<sup>2</sup> * 1 = 16 。
|
||||
所有英雄组的力量之和为 8 + 1 + 64 + 4 + 32 + 16 + 16 = 141 。
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>nums = [1,1,1]
|
||||
<b>输出:</b>7
|
||||
<b>解释:</b>总共有 7 个英雄组,每一组的力量都是 1 。所以所有英雄组的力量之和为 7 。
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= nums.length <= 10<sup>5</sup></code></li>
|
||||
<li><code>1 <= nums[i] <= 10<sup>9</sup></code></li>
|
||||
</ul>
|
||||
46
leetcode-cn/problem (Chinese)/计数器 II [counter-ii].html
Normal file
46
leetcode-cn/problem (Chinese)/计数器 II [counter-ii].html
Normal file
@@ -0,0 +1,46 @@
|
||||
<p>请你写一个函数 <code>createCounter</code>. 这个函数接收一个初始的整数值 <code>init</code> 并返回一个包含三个函数的对象。</p>
|
||||
|
||||
<p>这三个函数是:</p>
|
||||
|
||||
<ul>
|
||||
<li><code>increment()</code> 将当前值加 1 并返回。</li>
|
||||
<li><code>decrement()</code> 将当前值减 1 并返回。</li>
|
||||
<li><code>reset()</code> 将当前值设置为 <code>init</code> 并返回。</li>
|
||||
</ul>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong class="example">示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>init = 5, calls = ["increment","reset","decrement"]
|
||||
<b>输出:</b>[6,5,4]
|
||||
<strong>解释:</strong>
|
||||
const counter = createCounter(5);
|
||||
counter.increment(); // 6
|
||||
counter.reset(); // 5
|
||||
counter.decrement(); // 4
|
||||
</pre>
|
||||
|
||||
<p><strong class="example">示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<b>输入:</b>init = 0, calls = ["increment","increment","decrement","reset","reset"]
|
||||
<b>输出:</b>[1,2,1,0,0]
|
||||
<strong>解释:</strong>
|
||||
const counter = createCounter(0);
|
||||
counter.increment(); // 1
|
||||
counter.increment(); // 2
|
||||
counter.decrement(); // 1
|
||||
counter.reset(); // 0
|
||||
counter.reset(); // 0
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>-1000 <= init <= 1000</code></li>
|
||||
<li><code>总调用次数不会超过 1000</code></li>
|
||||
</ul>
|
||||
70
leetcode-cn/problem (Chinese)/频率跟踪器 [frequency-tracker].html
Normal file
70
leetcode-cn/problem (Chinese)/频率跟踪器 [frequency-tracker].html
Normal file
@@ -0,0 +1,70 @@
|
||||
<p>请你设计并实现一个能够对其中的值进行跟踪的数据结构,并支持对频率相关查询进行应答。</p>
|
||||
|
||||
<p>实现 <code>FrequencyTracker</code> 类:</p>
|
||||
|
||||
<ul>
|
||||
<li><code>FrequencyTracker()</code>:使用一个空数组初始化 <code>FrequencyTracker</code> 对象。</li>
|
||||
<li><code>void add(int number)</code>:添加一个 <code>number</code> 到数据结构中。</li>
|
||||
<li><code>void deleteOne(int number)</code>:从数据结构中删除一个 <code>number</code> 。数据结构 <strong>可能不包含</strong> <code>number</code> ,在这种情况下不删除任何内容。</li>
|
||||
<li><code>bool hasFrequency(int frequency)</code>: 如果数据结构中存在出现 <code>frequency</code> 次的数字,则返回 <code>true</code>,否则返回 <code>false</code>。</li>
|
||||
</ul>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>示例 1:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入</strong>
|
||||
["FrequencyTracker", "add", "add", "hasFrequency"]
|
||||
[[], [3], [3], [2]]
|
||||
<strong>输出</strong>
|
||||
[null, null, null, true]
|
||||
|
||||
<strong>解释</strong>
|
||||
FrequencyTracker frequencyTracker = new FrequencyTracker();
|
||||
frequencyTracker.add(3); // 数据结构现在包含 [3]
|
||||
frequencyTracker.add(3); // 数据结构现在包含 [3, 3]
|
||||
frequencyTracker.hasFrequency(2); // 返回 true ,因为 3 出现 2 次
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 2:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入</strong>
|
||||
["FrequencyTracker", "add", "deleteOne", "hasFrequency"]
|
||||
[[], [1], [1], [1]]
|
||||
<strong>输出</strong>
|
||||
[null, null, null, false]
|
||||
|
||||
<strong>解释</strong>
|
||||
FrequencyTracker frequencyTracker = new FrequencyTracker();
|
||||
frequencyTracker.add(1); // 数据结构现在包含 [1]
|
||||
frequencyTracker.deleteOne(1); // 数据结构现在为空 []
|
||||
frequencyTracker.hasFrequency(1); // 返回 false ,因为数据结构为空
|
||||
</pre>
|
||||
|
||||
<p><strong>示例 3:</strong></p>
|
||||
|
||||
<pre>
|
||||
<strong>输入</strong>
|
||||
["FrequencyTracker", "hasFrequency", "add", "hasFrequency"]
|
||||
[[], [2], [3], [1]]
|
||||
<strong>输出</strong>
|
||||
[null, false, null, true]
|
||||
|
||||
<strong>解释</strong>
|
||||
FrequencyTracker frequencyTracker = new FrequencyTracker();
|
||||
frequencyTracker.hasFrequency(2); // 返回 false ,因为数据结构为空
|
||||
frequencyTracker.add(3); // 数据结构现在包含 [3]
|
||||
frequencyTracker.hasFrequency(1); // 返回 true ,因为 3 出现 1 次
|
||||
</pre>
|
||||
|
||||
<p> </p>
|
||||
|
||||
<p><strong>提示:</strong></p>
|
||||
|
||||
<ul>
|
||||
<li><code>1 <= number <= 10<sup>5</sup></code></li>
|
||||
<li><code>1 <= frequency <= 10<sup>5</sup></code></li>
|
||||
<li>最多调用 <code>add</code>、<code>deleteOne</code> 和 <code>hasFrequency</code> <strong>共计</strong> <code>2 * 10<sup>5</sup></code> 次</li>
|
||||
</ul>
|
||||
Reference in New Issue
Block a user