mirror of
https://gitee.com/coder-xiaomo/leetcode-problemset
synced 2025-01-27 18:50:26 +08:00
58 lines
2.7 KiB
Markdown
58 lines
2.7 KiB
Markdown
|
|
探险家小扣终于来到了万灵之树前,挑战最后的谜题。
|
|||
|
|
已知小扣拥有足够数量的链接节点和 `n` 颗幻境宝石,`gem[i]` 表示第 `i` 颗宝石的数值。现在小扣需要使用这些链接节点和宝石组合成一颗二叉树,其组装规则为:
|
|||
|
|
- 链接节点将作为二叉树中的非叶子节点,且每个链接节点必须拥有 `2` 个子节点;
|
|||
|
|
- 幻境宝石将作为二叉树中的叶子节点,所有的幻境宝石都必须被使用。
|
|||
|
|
|
|||
|
|
能量首先进入根节点,而后将按如下规则进行移动和记录:
|
|||
|
|
- 若能量首次到达该节点时:
|
|||
|
|
- 记录数字 `1`;
|
|||
|
|
- 若该节点为叶节点,将额外记录该叶节点的数值;
|
|||
|
|
- 若存在未到达的子节点,则选取未到达的一个子节点(优先选取左子节点)进入;
|
|||
|
|
- 若无子节点或所有子节点均到达过,此时记录 `9`,并回到当前节点的父节点(若存在)。
|
|||
|
|
|
|||
|
|
如果最终记下的数依序连接成一个整数 `num`,满足 $num \mod~p=target$,则视为解开谜题。
|
|||
|
|
请问有多少种二叉树的组装方案,可以使得最终记录下的数字可以解开谜题
|
|||
|
|
|
|||
|
|
**注意:**
|
|||
|
|
- 两棵结构不同的二叉树,作为不同的组装方案
|
|||
|
|
- 两棵结构相同的二叉树且存在某个相同位置处的宝石编号不同,也作为不同的组装方案
|
|||
|
|
- 可能存在数值相同的两颗宝石
|
|||
|
|
|
|||
|
|
**示例 1:**
|
|||
|
|
> 输入:`gem = [2,3]`
|
|||
|
|
> `p = 100000007`
|
|||
|
|
> `target = 11391299`
|
|||
|
|
>
|
|||
|
|
> 输出:`1`
|
|||
|
|
>
|
|||
|
|
> 解释:
|
|||
|
|
> 包含 `2` 个叶节点的结构只有一种。
|
|||
|
|
> 假设 B、C 节点的值分别为 3、2,对应 target 为 11391299,如下图所示。
|
|||
|
|
> 11391299 % 100000007 = 11391299,满足条件;
|
|||
|
|
> 假设 B、C 节点的值分别为 2、3,对应 target 为 11291399;
|
|||
|
|
> 11291399 % 100000007 = 11291399,不满足条件;
|
|||
|
|
> 因此只存在 1 种方案,返回 1
|
|||
|
|
.gif){:height=300px}
|
|||
|
|
|
|||
|
|
|
|||
|
|
**示例 2:**
|
|||
|
|
> 输入:`gem = [3,21,3]`
|
|||
|
|
> `p = 7`
|
|||
|
|
> `target = 5`
|
|||
|
|
>
|
|||
|
|
> 输出:`4`
|
|||
|
|
>
|
|||
|
|
> 解释:
|
|||
|
|
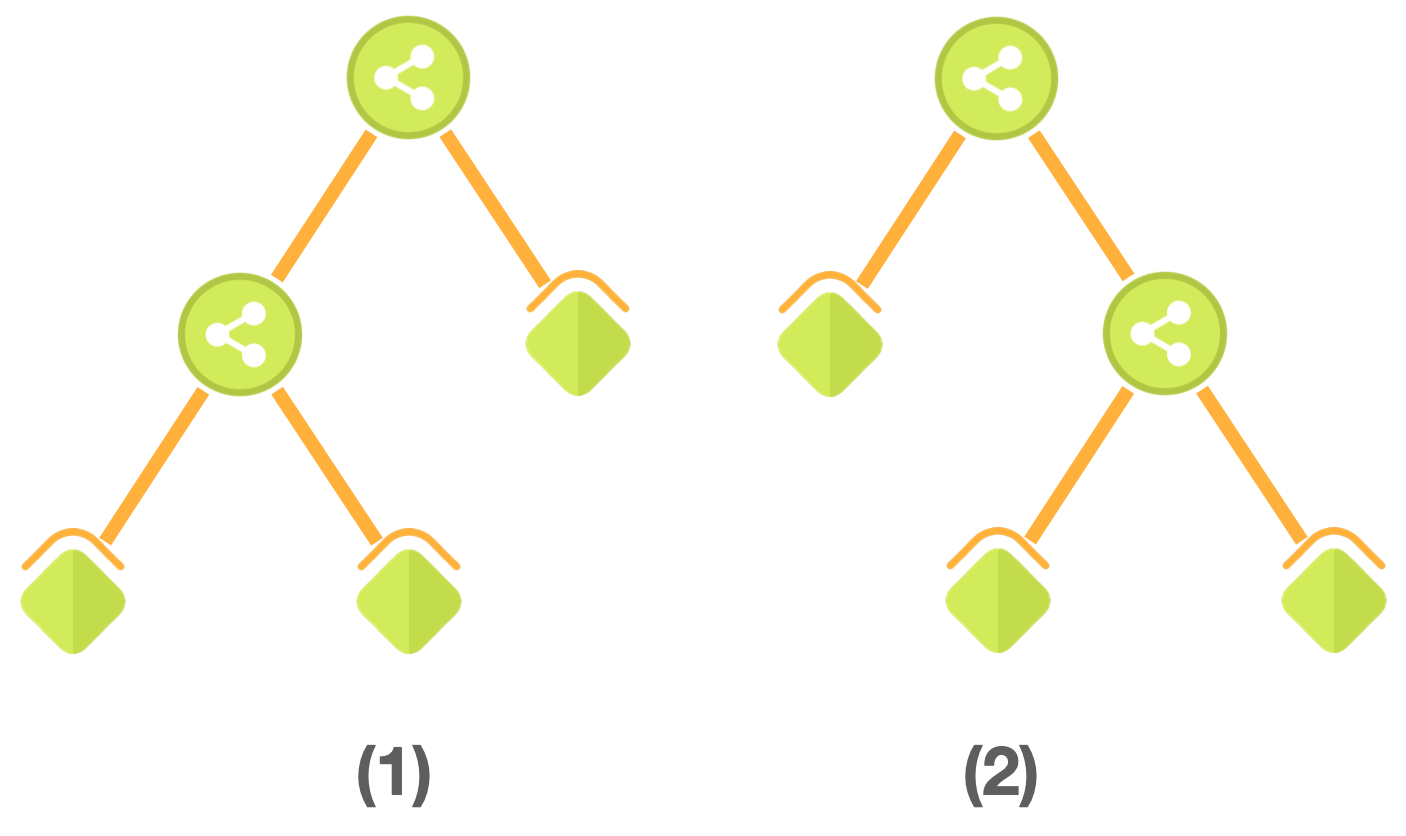
包含 `3` 个叶节点树结构有两种,列举如下:
|
|||
|
|
满足条件的组合有四种情况:
|
|||
|
|
> 当结构为下图(1)时:叶子节点的值为 [3,3,21] 或 [3,3,21],得到的整数为 `11139139912199`。
|
|||
|
|
> 当结构为下图(2)时:叶子节点的值为 [21,3,3] 或 [21,3,3],得到的整数为 `11219113913999`。
|
|||
|
|
{:width=500px}
|
|||
|
|
|
|||
|
|
|
|||
|
|
**提示:**
|
|||
|
|
- `1 <= gem.length <= 9`
|
|||
|
|
- `0 <= gem[i] <= 10^9`
|
|||
|
|
- `1 <= p <= 10^9`,保证 $p$ 为素数。
|
|||
|
|
- `0 <= target < p`
|
|||
|
|
- 存在 2 组 `gem.length == 9` 的用例
|